Merge sort – triedenie delením a spájaním v Java
Triediace algoritmy sa používajú na vzostupné alebo zostupné preusporiadanie prvkov poľa alebo zoznamu podľa numerického alebo lexikografického poradia. Triedenie je veľmi dôležité pre optimálny výkon iných algoritmov, ktoré vyžadujú triedené vstupné dáta.

V článku sa dozvieš:
Existuje množstvo rozličných triediacich algoritmov. Výber vhodného algoritmu závisí na faktoroch ako veľkosť a vlastnosti vstupných dát, dostupná pamäť a požiadavky na časovú a priestorovú náročnosť.
Aby sme ti uľahčili výber, predstavíme si v našom seriáli postupne najznámejšie algoritmy triedenia dát, vysvetlíme si ich princípy, výhody a nevýhody a naprogramujeme si ich v Jave.
Doteraz sme sa venovali nasledujúcim triediacim algoritmom:
- Triediace algoritmy: úvod do triedenia dát,
- Bubble sort – bublinkové triedenie,
- Comb sort – hrebeňové triedenie,
- Big O notácia: analýza zložitosti algoritmov,
- Selection sort – triedenie výberom.
- Insertion sort – triedenie vkladaním
- Counting sort – triedenie počítaním
- Heap sort – triedenie haldou
Dnes sa budeme venovať triedeniu pomocou spájania – mergovania (angl. Merge sort).
Merge sort
Merge sort je veľmi efektívny stabilný algoritmus triedenia, ktorý bol vynájdený v roku 1945 Johnom von Neumannom, jedným z priekopníkov v oblasti informatiky. Využíva techniku „rozdeľ a panuj“ (divide and conquer), základná myšlienka spočíva v tom, že ak máme komplexný problém snažíme sa ho rozložiť na menšie časti a tie vyriešime samostatne. Výsledné riešenie je teda výsledkom riešení jednotlivých menších podproblémov. Takéto rozloženie problémov sa potom dá výborne paralelizovať a efektívne riešiť na moderných viacjadrových procesoroch.
Vstupný vektor dát rozdelíme na niekoľko približne rovnakých častí. Najčastejšia verzia používa delenie na 2 časti, ide o binárny merge, v prípade viac častí ide o tzv. K-way merge. Poďme sa pozrieť, ako sa dá táto technika využiť pri triedení dát.
Merge sort algoritmus – princíp fungovania
Vstupné dáta sa rozdelia na približne dve rovnaké časti, ak je počet elementov nepárny, prvá časť má o 1 prvok viac. Každá s týchto častí poľa sa ďalej delí na polovicu a to sa opakuje až pokiaľ časť neobsahuje iba jeden prvok. Využíva sa pri tom rekurzívne volanie. Pole s jedným prvkom sa považuje sa zotriedené. Akonáhle sa dané časti už nedajú rozdeliť, tak sa vezmú obe posledné polovice a ich prvky sa spoja tak, aby aj výsledný zoznam zostal zotriedený. Toto sa opakuje, až dostane pôvodný vektor dát v zotriedenej podobe. Najlepšie to pochopíme na príklade na nasledujúcom obrázku.
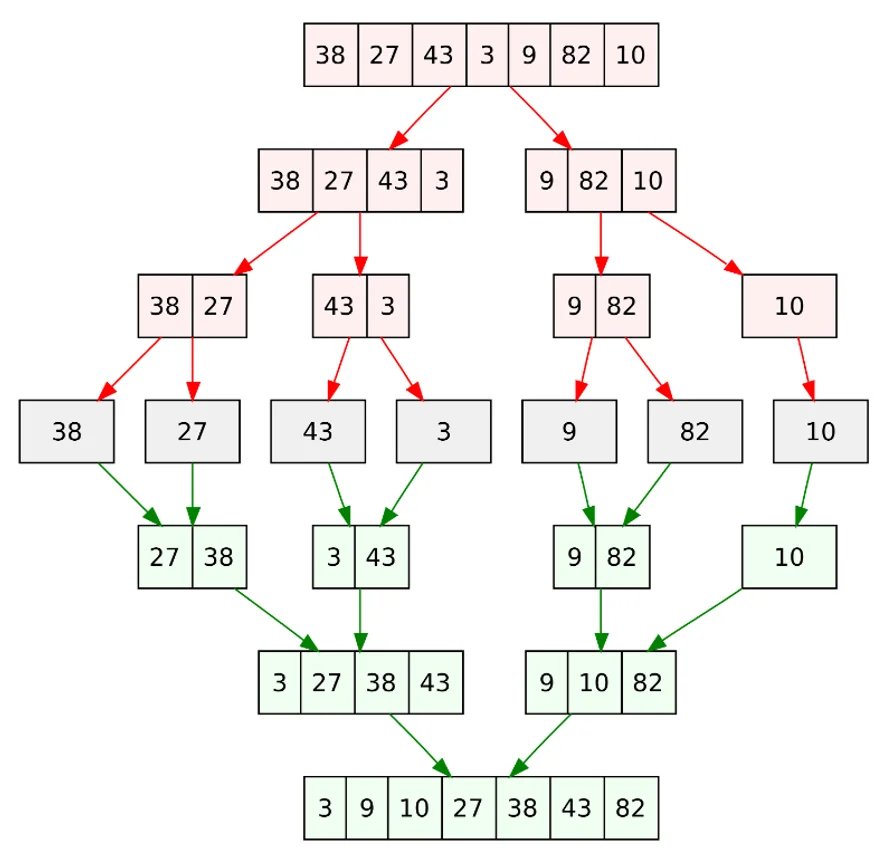
Merge sort animácie, vizualizácia, gif
Animácia merge sort vyzerá nasledovne:

Zdroj: commons.wikimedia.org/wiki/Category:Animations_of_sort_algorithms
Animáciu algoritmu nájdeš napríklad na stránke Toptal. Nachádza sa tam 8 typov algoritmov, animáciu si môžeš pustiť aj pozadu.
Na tejto stránke si môžeš prejsť jednotlivými krokmi algoritmu, vďaka čomu si vieš overiť časovú náročnosť algoritmu.
Výhody algoritmu Merge sort
- Stabilný algoritmus
- Efektívny aj obrovské sady dát
- Dá sa ľahko paralelizovať a rozložiť tak výpočtovú záťaž na viac procesorov
Nevýhody algoritmu Merge sort
- Na uloženie dát pri mergovaní podpolí sa vyžaduje dodatočný pamäťový priestor
Merge sort časová náročnosť
| Algoritmus | Metóda | Časová náročnosť | Pamäť | Stabilný | ||
| najhoršia | priemer | najlepšia | ||||
| Merge sort | mergovanie | O(n log n) | O(n log n) | O(n log n) | O(n) | áno |
Merge Sort implementácia, Java kód
Teraz si ukážeme implementáciu algoritmu Merge sort v Jave.
MergeSort.java
package sorting;
public class MergeSort {
public void sort(int data[], int left, int right)
{
if (left < right) {
// Find the cutting point
int middle = (left + right) / 2;
// Sort first and second part separately
sort(data, left, middle);
sort(data, middle + 1, right);
// Merge both sorted halves
merge(data, left, middle, right);
}
}
public void merge(int[] data, int left, int middle, int right) {
// Calculate sizes of left and right merge arrays
int leftPartSize = middle - left + 1;
int rightPartSize = right - middle;
// Create them
int[] leftPart = new int[leftPartSize];
int[] rightPart = new int[rightPartSize];
// Fill them
for (int i = 0; i < leftPartSize; i++) {
leftPart[i] = data[left + i];
}
for (int j = 0; j < rightPartSize; j++) {
rightPart[j] = data[middle + 1 + j];
}
System.out.print("L: ");
printArray(leftPart);
System.out.print("+ R: ");
printArray(rightPart);
System.out.print("=> ");
// k is index of merged array
int i = 0, j = 0, k = left;
while (i < leftPartSize && j < rightPartSize) {
if (leftPart[i] <= rightPart[j]) {
data[k++] = leftPart[i++];
}
else {
data[k++] = rightPart[j++];
}
}
// Copy any remaining elements
while (i < leftPartSize) {
data[k++] = leftPart[i++];
}
while (j < rightPartSize) {
data[k++] = rightPart[j++];
}
for (i = left; i < k; i++)
System.out.print(data[i] + " ");
System.out.println();
}
// Function to print an array
public void printArray(int data[])
{
for (int i = 0; i < data.length; i++)
System.out.print(data[i] + " ");
//System.out.println();
}
}Main.java
import sorting.MergeSort;
public class Main {
public static void main(String[] args) {
int dataToSort[] = { 6, 5, 4, 2, 3, 1, 7 };
MergeSort mergeSort = new MergeSort();
System.out.print("Input: ");
mergeSort.printArray(dataToSort);
System.out.println("");
mergeSort.sort(dataToSort, 0, dataToSort.length - 1);
System.out.print("Sorted: ");
mergeSort.printArray(dataToSort);
}
}Výstup z tohto príkladu je:

Pripravili sme pre teba súbory so spomínaným príkladom vo forme kódu, ktorý si môžeš spustiť priamo v Jave. Stiahni si kód Java MergeSort tu.
Ak si Java programátor a hľadáš prácu, pozri si naše benefity pre zamestnancov a reaguj na najnovšie ponuky práce.


