Merge sort algorithm Java
Sorting algorithms are used to reorder the elements of an array or list in ascending or descending numerical or lexicographic order. Sorting is very important for the optimal performance of other algorithms that require sorted input data.

V článku sa dozvieš:
There are many different sorting algorithms. The selection of an appropriate algorithm depends on factors such as the size and characteristics of the input data, available memory, and time and space complexity.
To make your choice easier, in our series we will introduce the most well-known data sorting algorithms, explain their principles, advantages and disadvantages, and program them in Java.
So far, we have discussed the following:
- Sorting algorithms: Introduction to data sorting
- Bubble sort
- Comb sort
- Big O notation
- Selection sort
- Insertion sort
- Counting sort
- Heap sort
Today we are going to look at merge sort.
Merge sort meaning
Merge sort is a very efficient stable sorting algorithm that was invented in 1945 by John von Neumann, one of the pioneers in the field of computer science. It uses the divide and conquer technique, the basic idea is that if we have a complex problem we try to break it down into smaller parts and solve those parts separately. The final solution is therefore the result of solving each of the smaller sub-problems. Such a decomposition of problems can then be perfectly parallelized and solved efficiently on modern multi-core processors.
We divide the input data vector into several approximately equal parts. The most common version uses a 2-part partitioning, this is a binary merge, in the case of multiple parts it is a so-called K-way merge. Let’s see how this technique can be used in data sorting.
How merge sort works
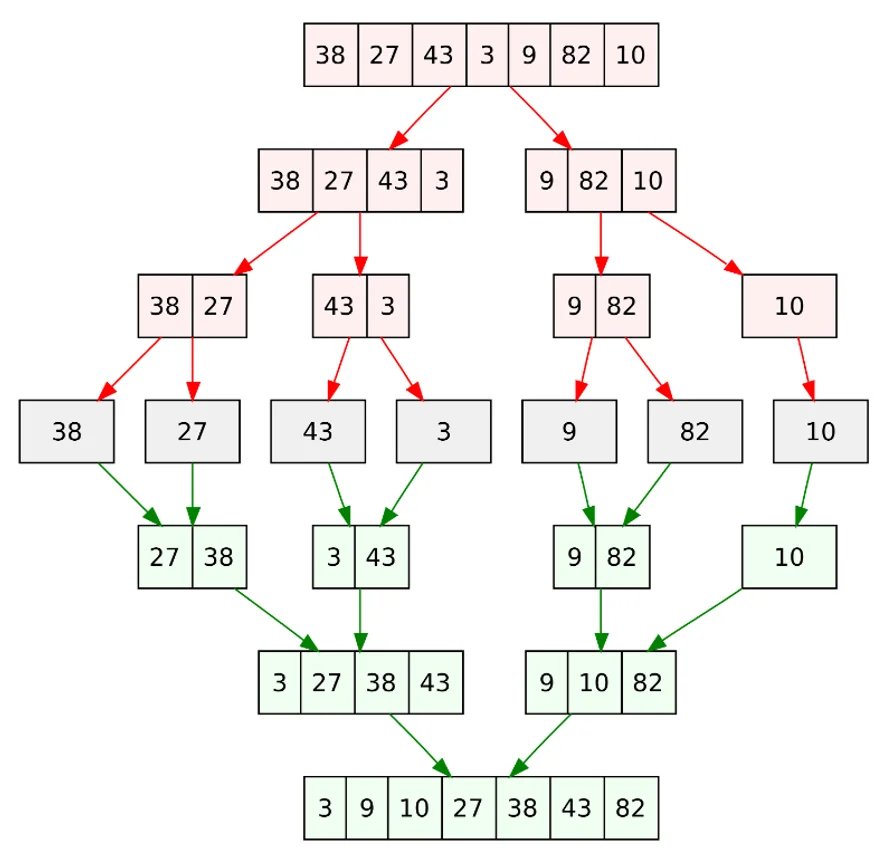
The input data is divided into approximately two equal parts, if the number of elements is odd, the first part has 1 more element. Each of these parts of the array is further divided in half and this is repeated until the part contains only one element. This uses a recursive call. An array with one element is considered to be sorted. Once the parts can no longer be split, the last two halves are taken and their elements are merged so that the resulting list remains sorted as well. This is repeated until the original data vector is received in sorted form. This is best understood with the example in the following figure.
Merge sort animation, visualization, gif
The merge sort animation looks like this:

Source: commons.wikimedia.org/wiki/Category:Animations_of_sort_algorithms
Visit Toptal for interactive visualizations. There are 8 types of algorithms and you can also play the animation backwards.
On this page you can go through the steps of the algorithm to check the time taken by the algorithm.
Merge sort algorithm advantages
- Stable algorithm
- Efficient even for huge data sets
- Can be easily parallelized to spread the computational load across multiple processors
Merge sort algorithm disadvantages
- Additional memory space is required to store data when merging subarrays
Merge sort time complexity
| Algorithm | Method | Time Complexity | Memory | Stable | ||
| worst | average | best | ||||
| Merge sort | merging | O(n log n) | O(n log n) | O(n log n) | O(n) | Yes |
Merge sort Java implementation
Now we will show the implementation of the merge sort algorithm in Java.
MergeSort.java
package sorting;
public class MergeSort {
public void sort(int data[], int left, int right)
{
if (left < right) {
// Find the cutting point
int middle = (left + right) / 2;
// Sort first and second part separately
sort(data, left, middle);
sort(data, middle + 1, right);
// Merge both sorted halves
merge(data, left, middle, right);
}
}
public void merge(int[] data, int left, int middle, int right) {
// Calculate sizes of left and right merge arrays
int leftPartSize = middle - left + 1;
int rightPartSize = right - middle;
// Create them
int[] leftPart = new int[leftPartSize];
int[] rightPart = new int[rightPartSize];
// Fill them
for (int i = 0; i < leftPartSize; i++) {
leftPart[i] = data[left + i];
}
for (int j = 0; j < rightPartSize; j++) {
rightPart[j] = data[middle + 1 + j];
}
System.out.print("L: ");
printArray(leftPart);
System.out.print("+ R: ");
printArray(rightPart);
System.out.print("=> ");
// k is index of merged array
int i = 0, j = 0, k = left;
while (i < leftPartSize && j < rightPartSize) {
if (leftPart[i] <= rightPart[j]) {
data[k++] = leftPart[i++];
}
else {
data[k++] = rightPart[j++];
}
}
// Copy any remaining elements
while (i < leftPartSize) {
data[k++] = leftPart[i++];
}
while (j < rightPartSize) {
data[k++] = rightPart[j++];
}
for (i = left; i < k; i++)
System.out.print(data[i] + " ");
System.out.println();
}
// Function to print an array
public void printArray(int data[])
{
for (int i = 0; i < data.length; i++)
System.out.print(data[i] + " ");
//System.out.println();
}
}Main.java
import sorting.MergeSort;
public class Main {
public static void main(String[] args) {
int dataToSort[] = { 6, 5, 4, 2, 3, 1, 7 };
MergeSort mergeSort = new MergeSort();
System.out.print("Input: ");
mergeSort.printArray(dataToSort);
System.out.println("");
mergeSort.sort(dataToSort, 0, dataToSort.length - 1);
System.out.print("Sorted: ");
mergeSort.printArray(dataToSort);
}
}The output of this merge sort Java example is:

We have prepared the files with the above example as code that you can run directly in Java. Download the Java MergeSort code here.
If you’re a Java developer looking for a job, check out our employee benefits and respond to our job offers!


