V dnešnom digitálnom svete sa dáta stali jednou z najcennejších komodít. Či už ide o sociálne siete, ktoré denne analyzujú miliardy interakcií medzi komunikujúcimi ľuďmi vo virtuálnom priestore internetu, o zdravotnícke systémy ukladajúce informácie o pacientoch a chorobách, ktorí prišli k lekárovi na vyšetrenie, alebo o digitálne obchodné inštrumenty ako Bitcoin, ktorý práve atakuje magickú úroveň sto tisíc dolárov za jeden Bitcoin.

Dáta sú všadeprítomné a stávajú sa hybnou silou inovácií vo všetkých oblastiach ľudskej činnosti. Ich efektívne využitie však vyžaduje porozumenie ich štruktúre a spracovaniu – čo nás privádza k dátovým štruktúram. Samotné dáta by nám boli zbytočné, ak by sme nepoznali spôsob, ako ich efektívne organizovať, uchovávať a spracovávať.

Predstavme si knižnicu bez akéhokoľvek systému usporiadania kníh – chaos, v ktorom je takmer nemožné nájsť, čo hľadáme. Podobne by svet počítačových systémov nedokázal zvládať súčasný objem dát, bez premyslených a optimalizovaných dátových štruktúr.

Tieto štruktúry, ktoré sú pre nás používateľov neviditeľnou architektúrou, sú zodpovedné za správnu kategorizáciu dát, uloženie a spracovanie takým spôsobom, aby napr. sekretárke pracujúcej s kancelárskym softvérom, hráčovi najnovšej počítačovej hry, zákazníkovi nakupujúci počas Black Friday v online obchode, či programátorovi dopytov vo veľkej databáze, priniesli takmer okamžite presne tie dáta, ktoré práve v danom okamihu potrebujú alebo očakávajú.

V tomto článku sa ponoríme do fascinujúceho sveta dátových štruktúr. Povieme si o tých základných, ako sú polia a zoznamy. Od tých základných, ako sú polia a zoznamy, až po pokročilé, ako hashovacie tabuľky alebo binárne stromy, ukážeme si, ako každá z nich hrá kľúčovú rolu v riešení rôznych výpočtových problémov. Dozvieš sa, prečo sú niektoré štruktúry ideálne na rýchle vyhľadávanie, iné na ukladanie veľkého množstva údajov a ďalšie na dynamickú správu dát.

Bez ohľadu na to, či si začínajúci programátor, zvedavý študent informatiky, ktorý chce lepšie pochopiť základy svojho budúceho remesla alebo už pracuješ v IT oblasti, tento článok ti poskytne praktický pohľad na dôležitosť správneho výberu dátových štruktúr.

Nepochopením kľúčových vlastností, silných a slabých stránok tej ktorej dátovej štruktúry a ich nevhodným, neefektívnym použitím strácame nielen drahocenný čas spracovania dát, ale aj plytváme hardvérovými prostriedkami. Ako všetci vieme, čas sú peniaze a napr. pomalá odozva pri vyhľadávaní tovaru na e-shope (tým chápeme spracovanie a vyfiltrovanie dát podľa zadaných kritérií používateľa) odradila od nákupu už nejedného zákazníka.

Dáta nie sú len bezvýznamne binárne čísla alebo text zložený z podivných ASCII znakov – sú základom nášho života. Svet moderných technológií poháňajú dáta, efektívne dátové štruktúry a algoritmy a tento článok ti niektoré z nich predstaví.

Čo sú dáta?

Dáta predstavujú základné stavebné kamene informácií. Sú to obyčajné fakty, čísla, texty, symboly, zvuky či obrazy, ktoré nemajú bez kontextu žiadny konkrétny význam. Môžeme si ich predstaviť ako jednotlivé dieliky puzzle – samostatne sú len malými časťami celku, no keď ich správne usporiadame, môžu vytvoriť krásny obrázok alebo stať sa pevným základom niečo väčšieho.

Charakteristika dát

• Surovosť: Dáta sú neinterpretované. Napríklad číslo „42“ samo o sebe nehovorí veľa – môže ísť o vek, počet strán v knihe, alebo len náhodné číslo.
• Potenciál pre informáciu: Keď sa dáta spracujú, analyzujú alebo umiestnia do kontextu, premieňajú sa na informácie. Napríklad „42 °C“ v kontexte počasia naznačuje extrémne teplo.
• Digitálny zápis: V modernej informatike sú dáta reprezentované digitálne – vo forme binárnych hodnôt (0 a 1), ktoré sú základom počítačových operácií.

Kategórie dát

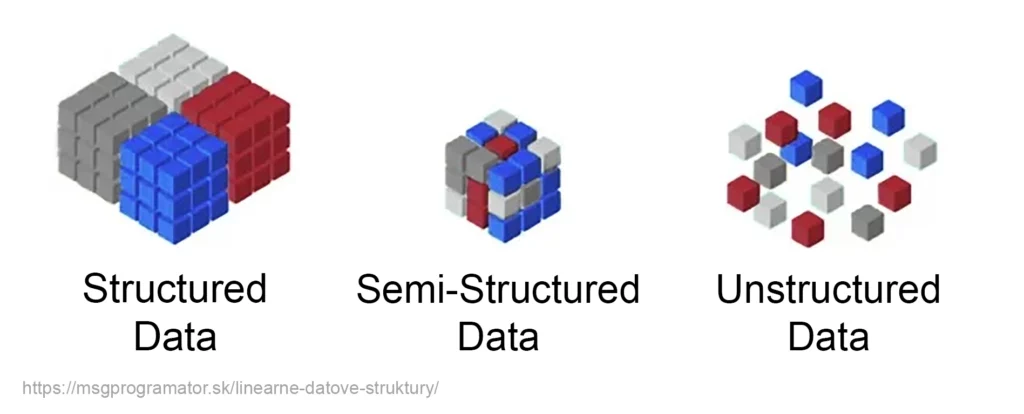
Dáta si vieme rozdeliť na základe štruktúrovanosti nasledovne:

• Štruktúrované dáta – dáta uložené v organizovanej forme, ako sú tabuľky alebo databázy, kde sú jednotlivé hodnoty priradené konkrétnym atribútom.
• Neštruktúrované dáta – textové dokumenty, obrázky, videá alebo zvukové záznamy, ktoré nemajú preddefinovanú štruktúru.
• Semi-štruktúrované dáta – dáta, ktoré majú určitú organizačnú štruktúru, napríklad XML alebo JSON súbory, ale nie sú tak prísne štruktúrované ako tabuľky.

Význam dát

Dáta tvoria základ všetkých rozhodnutí v modernom svete. Firmy ich využívajú na analýzu trhu, vedci na výskum, lekári na diagnostiku a liečbu a vlády na plánovanie rozpočtov. Umelá inteligencia (AI) ako ju dnes poznáme by bez nich nikdy nevznikla. Vďaka technológiám, ktoré umožňujú zber, spracovanie a analýzu obrovského množstva dát, sme dnes schopní odhaľovať vzorce, robiť predpovede a pomocou štatistiky nachádzať nové znalosti, ktoré by inak zostali skryté.

Dátové štruktúry

Dátové štruktúry predstavujú spôsob organizácie, uchovávania a spracovania dát tak, aby sa dali efektívne používať v počítačových programoch. Poskytujú dátam určitú formu a určujú, ako budú dáta usporiadané, ale aj ako s nimi bude možné manipulovať. Sú základnými stavebnými kameňmi programu.

Zásady návrhu dátových štruktúr

Vždy sa pri návrhu dátovej štruktúry, alebo pri výbere nejakej existujúcej snažíme optimalizovať rýchlosť operácií ako vyhľadávanie dát, ich načítanie a zápis. Sekundárne treba pamätať na to, že efektívne dátové štruktúry by mali minimalizovať pamäťovú náročnosť. To zahŕňa nielen priestor pre uloženie dát, ale aj pomocných štruktúr, indexov alebo metadát, ktoré pomáhajú pri rýchlejšom vyhľadávaní práve požadovaných informácií. Implementácia dátovej štruktúry by mala byť pre dané dáta, čo najjednoduchšia, aby sa eliminovalo riziko chýb. Rovnako podstatné je navrhnúť dátovú štruktúru tak, aby bola flexibilná a ľahko rozšíriteľná pre rôzne aplikácie.

Efektívny výber a implementácia údajových štruktúr má zásadný vplyv na zložitosť algoritmov, ktoré ich využívajú a teda celkový výkon aplikácie.

Typy dátových štruktúr

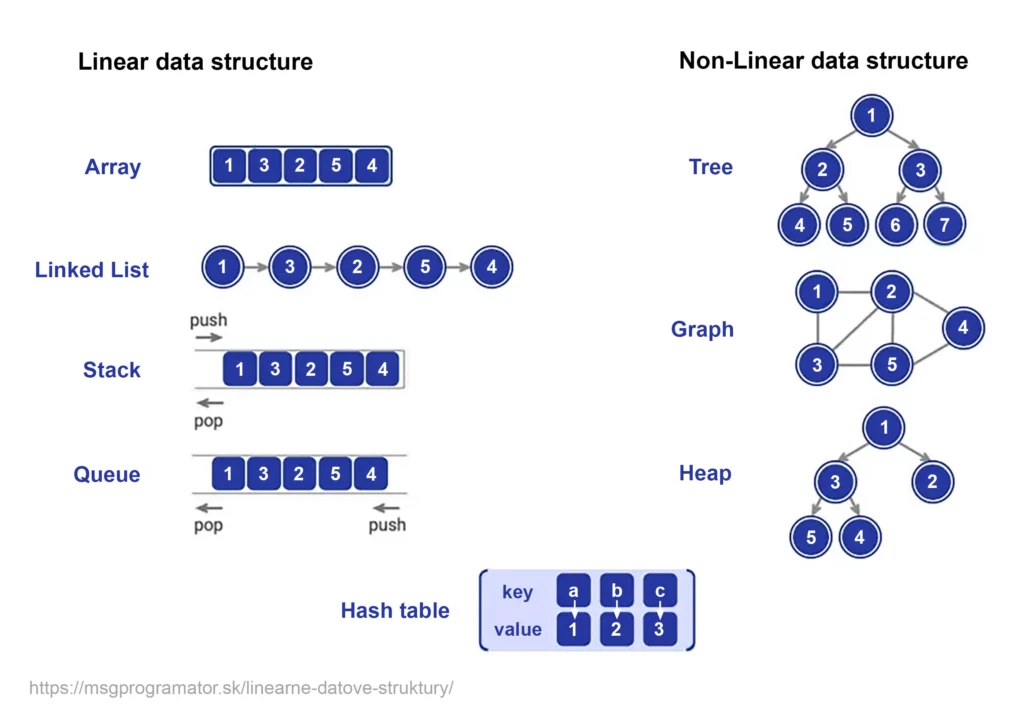
Dátové štruktúry môžeme rozdeliť podľa ich architektúry ukladania dát na:

• Lineárne dátové štruktúry
  V lineárnej dátovej štruktúre sú všetky prvky usporiadané v lineárnom alebo sekvenčnom poradí. Typickými príkladmi tohto typu štruktúry sú: pole (array), spájaný zoznam (linked list), zásobník (stack), fronta (queue).
• Nelineárne dátové štruktúry
  V nelineárnej dátovej štruktúre sú elementy usporiadané hierarchicky alebo do viacúrovňovej komplexnej dátovej štruktúry. Typickým príkladom tohto typu štruktúry sú: strom (tree) a graf (graph).
• Tabuľkové dátové štruktúry
  Sem patria dátové štruktúry fungujúce na princípoch hashovacej tabuľky (hash table).

Základné operácie s dátovými štruktúrami

Vyhľadávanie (search) – možno vyhľadať akýkoľvek prvok v dátovej štruktúre.
Vloženie (insert) – vkladanie nového prvku do dátovej štruktúry.
Aktualizácia (update) – nahradenie prvku iným prvkom v dátovej štruktúre.
Odstránenie (delete) – odstránenie existujúceho prvku z dátovej štruktúry.
Triedenie (sort) – prvky dátovej štruktúry možno triediť buď vzostupne alebo zostupne. V našich minulých článkoch sme sa vyčerpávajúco venovali triedeniu dát a triediacim algoritmom.

Abstraktný dátový typ vs. Dátová štruktúra

Dátová štruktúra sa niekedy nesprávne zamieňa za abstraktný dátový typ (ADT).

ADT hovorí, čo sa má urobiť, a dátová štruktúra hovorí, ako sa to má urobiť. Inými slovami, môžeme povedať, že ADT nám poskytuje návrh, zatiaľ čo dátová štruktúra poskytuje implementačnú časť. V konkrétnom ADT môžu byť implementované rôzne dátové štruktúry. Napr. ADT zásobník môže na dátovej úrovni využívať dátovú štruktúru pole, alebo pospájaný zoznam (linked list). Rozhodnutie, čo sa použije je na programátorovi a jeho špecifických požiadavkách.

Lineárne dátové štruktúry

Teraz si podrobne rozoberieme lineárne dátové štruktúry, ich základne vlastnosti, typy, výhody a nevýhody, ako aj najčastejšie prípady/príklady použitia.

Pole (Array)

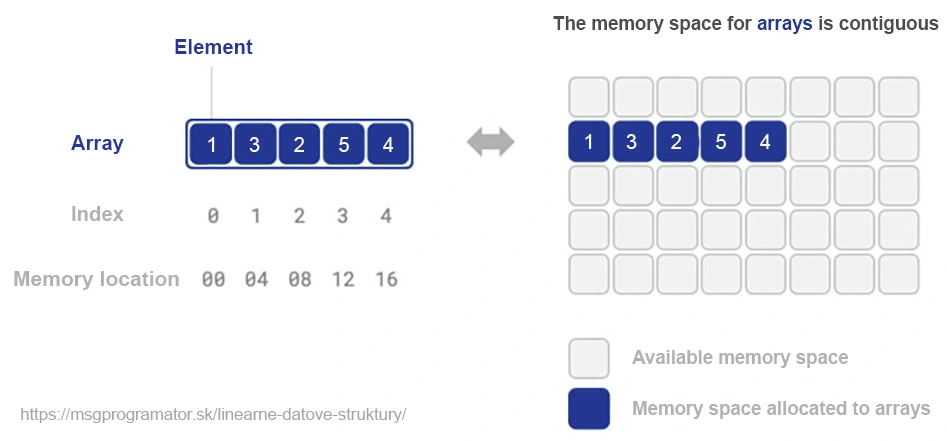
V programovaní sú polia jednou z najnákladnejších a najpoužívanejších dátových štruktúr. Ukladajú prvky v súvislom bloku pamäte, pričom každý prvok je prístupný pomocou číselného indexu. Zatiaľ čo polia ponúkajú prístupový čas O(1), čo je vynikajúce pre operácie náročné na čítanie, efektívnosť operácií zápisu (vkladanie a mazanie) sa môže výrazne líšiť v závislosti od umiestnenia operácie v poli a celkovej veľkosti poľa.

Základné vlastnosti poľa

• Pevná veľkosť: Po deklarovaní poľa je jeho veľkosť fixná a nemožno ju počas behu meniť. Preto potrebujeme dopredu vedieť, koľko prvkové pole treba vytvoriť. Avšak v Jave sa toto obmedzenie dá obísť použitím dynamickej štruktúry poľa ArrayList.
• Homogénne prvky: Polia zvyčajne ukladajú prvky rovnakého dátového typu, čím sa zabezpečuje jednotnosť uložených údajov.
• Súvislá alokácia pamäte: Prvky sú uložené v pamäťových miestach alokovaných za sebou, čo umožňuje efektívny prístup k prvkom pomocou indexov.

Typy polí

1. Jednorozmerné polia (One-Dimensional arrays) – rada prvkov uložených za sebou.
2. Viacrozmerné polia (Multidimensional arrays) – polia, ktoré obsahujú jedno alebo viac polí ako svoje prvky. To umožňuje vytvárať dátovú reprezentáciu vo viacerých dimenziách. Napr. 2D pole sa používa pre matice.

Výhody použitia poľa

• Priamy prístup k prvkom: Priamy prístup k akémukoľvek prvku pomocou jeho indexu poskytuje efektívne operácie čítania.
• Pamäťová efektívnosť: Je veľmi efektívne na ukladanie veľkého počtu prvkov za sebou. Netreba alokovať extra pamäť pre referencie na ďalšie prvky ako pri pospájanom zozname.

Nevýhody použitia poľa

• Pevná veľkosť: Veľkosť statického poľa je určená v čase kompilácie, kvôli čomu je táto štruktúra neflexibilná.
• Neefektívne vkladanie a odstraňovanie: Najmä pre prvky na začiatku alebo v strede poľa, pretože to vyžaduje posúvanie prvkov.
• Plytvanie pamäťou: Ak nie je plne využité, zbytočne blokuje pamäť.

Použitie poľa

• Ukladanie údajov: Hlavne takých, ktoré boli predtým zotriedené a nebude sa meniť ich poradie v poli.
• Vyhľadávacie tabuľky: Polia môžu efektívne implementovať vyhľadávacie tabuľky, ktoré umožňujú rýchly prístup k vopred vypočítaným hodnotám.
• Implementácia iných dátových štruktúr: Pole je základná štruktúra pre zložitejšie dátové štruktúry, ako sú haldy, hašovacie tabuľky a dynamické polia (napr. Java Vector).
• Algoritmy: Používajú sa v širokej škále algoritmov, vrátane triediacich a vyhľadávacích algoritmov, kde náhodný prístup k prvkom výrazne optimalizuje výkon.

Zoznam (Linked List)

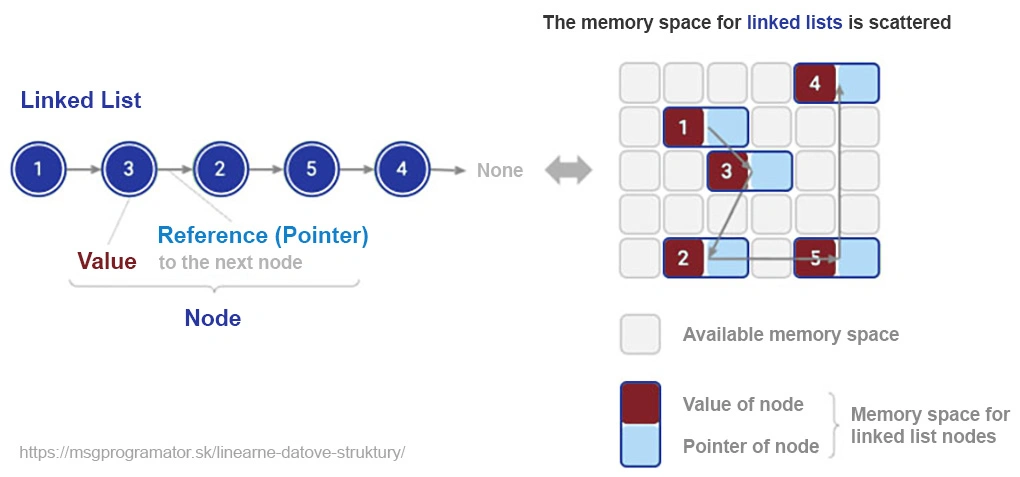
Spájaný zoznam je základná dátová štruktúra, ktorá sa odlišuje od poľa svojou dynamickou povahou a flexibilitou. Na rozdiel od polí, ktoré vyžadujú súvislý blok pamäte, zoznam pozostáva z uzlov rozptýlených v pamäti, pričom každý uzol obsahuje hodnotu a referenciu (ukazovateľ) na ďalší uzol. Táto vlastnosť umožňuje jednoduchú manipuláciu s prvkami, ale za cenu nižšej efektivity pri priamom prístupe.

Základné vlastnosti zoznamu

• Dynamická veľkosť: Veľkosť zoznamu nie je pevne daná a môže sa počas behu programu dynamicky meniť – zoznam sa hodí ideálne na aplikácie, kde nie je vopred známa veľkosť dát.
• Rozptýlená alokácia pamäte: Uzly zoznamu nie sú uložené v súvislých pamäťových blokoch, ale sú prepojené cez odkazy, čo umožňuje pridávanie a mazanie prvkov bez potreby preskupovania pamäte.
• Sekvenčný prístup: Na rozdiel od polí, ktoré umožňujú priamy prístup k prvkom cez index, zoznam vyžaduje postupné prechádzanie od začiatku až po požadovaný uzol.

Typy zoznamov

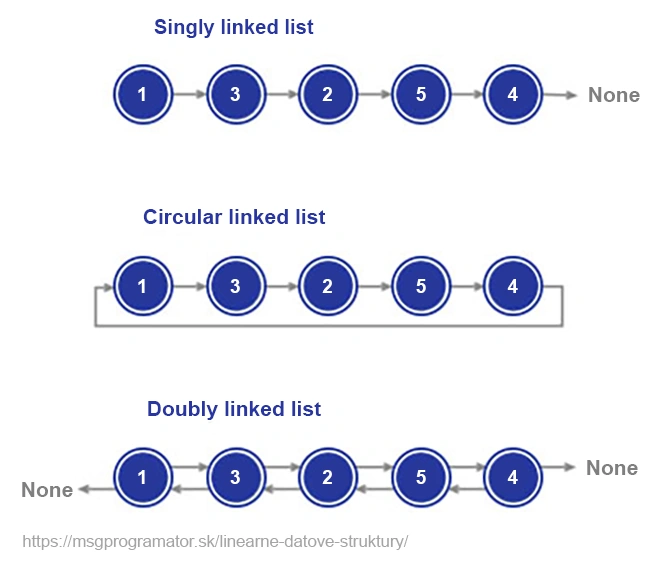
• Jednosmerný zoznam (Singly listed list): Každý uzol obsahuje hodnotu a odkaz na ďalší uzol. Posledný uzol ukazuje na null, čím indikuje koniec zoznamu.
• Kruhový zoznam (Circular listed list): Posledný uzol ukazuje späť na prvý uzol, čím vytvára kruh – užitočný pri aplikáciách, ktoré vyžadujú opakovaný prístup k prvkom.
• Obojstranný zoznam (Doubly listed list): Každý uzol obsahuje odkaz na predchádzajúci a nasledujúci uzol, čo umožňuje prechod oboma smermi.

Výhody použitia zoznamu

• Efektívna manipulácia: Pridávanie a mazanie prvkov je jednoduché a efektívne, ak poznáme referenciu na miesto úpravy, s časovou zložitosťou O(1).
• Flexibilita: Dynamická veľkosť eliminuje potrebu špecifikovať kapacitu dopredu a vyhýba sa plytvaniu pamäťou.
• Implementácia komplexných štruktúr: Zoznamy sú základom pre iné dátové štruktúry, ako sú zásobníky, fronty a grafy.

Nevýhody použitia zoznamu

• Pomalý prístup: Náhodný prístup k prvkom nie je možný – každý prístup vyžaduje prechod od začiatku zoznamu, čo má časovú zložitosť O(n).
• Pamäťová náročnosť: Každý uzol vyžaduje dodatočnú pamäť na uloženie referencií, čo môže byť neefektívne pri veľkom množstve malých prvkov.
• Zložitejšia správa: Manipulácia s ukazovateľmi pri pridávaní alebo mazaní uzlov môže byť náchylná na chyby.

Použitie zoznamu

• Dynamické dátové štruktúry: Zoznamy sa využívajú tam, kde sa dáta často pridávajú alebo odstraňujú, napríklad pri úlohách, kde sa neustále mení počet prvkov.
• Reprezentácia matematických štruktúr: Používajú sa na reprezentáciu polynómov alebo iných dynamických množín údajov.
• Implementácia zásobníkov a frontov: Mnohé dátové štruktúry sú postavené práve na pospájaných zoznamoch.
• Garbage collection: Algoritmy na správu pamäte, ako napríklad mark-and-sweep, využívajú zoznamy na evidenciu blokov pamäte.

Príklady použitia

Predstav si správu histórie v prehliadači. Každý navštívený web je uložený ako uzol v zozname. Keď sa vrátiš späť na predchádzajúcu stránku, jednoducho sa pohneš na predchádzajúci uzol, čo je ideálny príklad, kde zoznam exceluje. Zoznamy sú nenahraditeľné pri úlohách vyžadujúcich flexibilitu a dynamické operácie s dátami, napriek tomu, že nie sú vhodné na všetky typy úloh.

Zásobník (Stack)

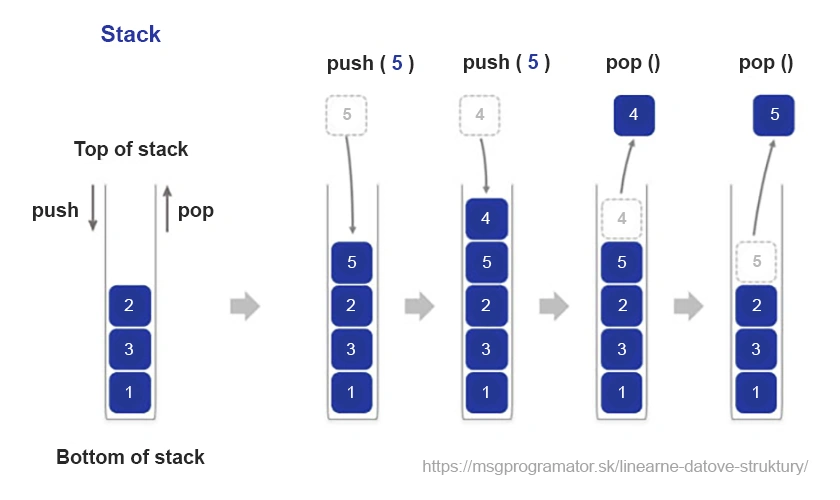
Zásobník je jednou zo základných dátových štruktúr, ktorá funguje na princípe „posledný dovnútra, prvý von“ (LIFO – Last In, First Out). Predstavme si ho ako sadu tanierov uložených na sebe – nový tanier pridáme vždy navrch a pri odoberaní vždy siahneme po tom vrchnom. Táto jednoduchá, no mimoriadne užitočná štruktúra má široké využitie v oblasti programovania a informatiky.

Základné vlastnosti zásobníka

• Operácie len na vrchole: Všetky operácie (pridanie a odobratie prvku) sa vykonávajú na vrchole zásobníka, čím sa udržiava jeho LIFO charakter.
• Dynamická veľkosť: V závislosti od implementácie (napríklad pomocou zoznamu) môže zásobník dynamicky rásť alebo sa zmenšovať počas behu programu.
• Sekvenčný prístup: Na rozdiel od polí nemá zásobník náhodný prístup – priamo pracovať môžeme iba s posledným vloženým prvkom.

Kľúčové operácie zásobníka

• Push: Pridá prvok na vrchol zásobníka.
  Pop: Odstráni a vráti prvok z vrcholu zásobníka.
  Peek (Top): Zobrazí prvok na vrchole zásobníka bez jeho odstránenia.
  IsEmpty: Skontroluje, či je zásobník prázdny.

Výhody použitia zásobníka

• Rýchlosť operácií: Operácie pridávania a odoberania prvkov sú veľmi efektívne, s časovou zložitosťou O(1).
• Jednoduchosť implementácie: Zásobník je jednoduchý na pochopenie a implementáciu, či už pomocou poľa alebo zoznamu.
• Špecifické využitie: Zásobník je ideálny na riešenie problémov, kde treba zachovať poradie spracovania v štýle LIFO.

Nevýhody použitia zásobníka

• Obmedzený prístup: Prístup je možný iba k prvku na vrchole, čo ho robí nevhodným na úlohy vyžadujúce priame prístupy.
• Pamäťová závislosť: V prípade implementácie pomocou poľa môže zásobník vyžadovať opätovné alokovanie pamäte, ak jeho kapacita prekročí pôvodnú veľkosť.

Použitie zásobníka

• Správa funkčných volaní: Zásobníky sa používajú na správu volaní funkcií v programoch. Pri každom volaní funkcie sa jej kontext ukladá na zásobník, a po jej ukončení sa obnovuje.
• Kontrola syntaxe: Pri overovaní správneho uzatvárania zátvoriek alebo iných párových symbolov v kóde zásobník zabezpečuje správnosť poradia.
• Algoritmy na spätné prehľadávanie (backtracking): Používajú sa pri úlohách, ako je riešenie bludísk alebo Sudoku, kde sa treba vrátiť na predchádzajúci bod rozhodovania.
• Implementácia funkcií undo: V aplikáciách, kde chceme vrátiť späť poslednú akciu, zásobník uchováva históriu vykonaných krokov.

Príklad použitia

Predstavme si editor textu s funkciou naspäť. Každá zmena, ktorú vykonáme, sa pridá na zásobník. Keď klikneme na „späť“, posledná zmena sa odstráni a náš dokument sa vráti do predchádzajúceho stavu.

Zásobníky sú síce špecifické svojou jednoduchosťou a obmedzeniami, no práve vďaka týmto vlastnostiam sú nenahraditeľné v mnohých aplikáciách a algoritmoch, kde treba presne zachovať poradie vykonávania operácií. Pre viac informácií si prečítaj článok o zásobníku Java Stack.

Front (Queue)

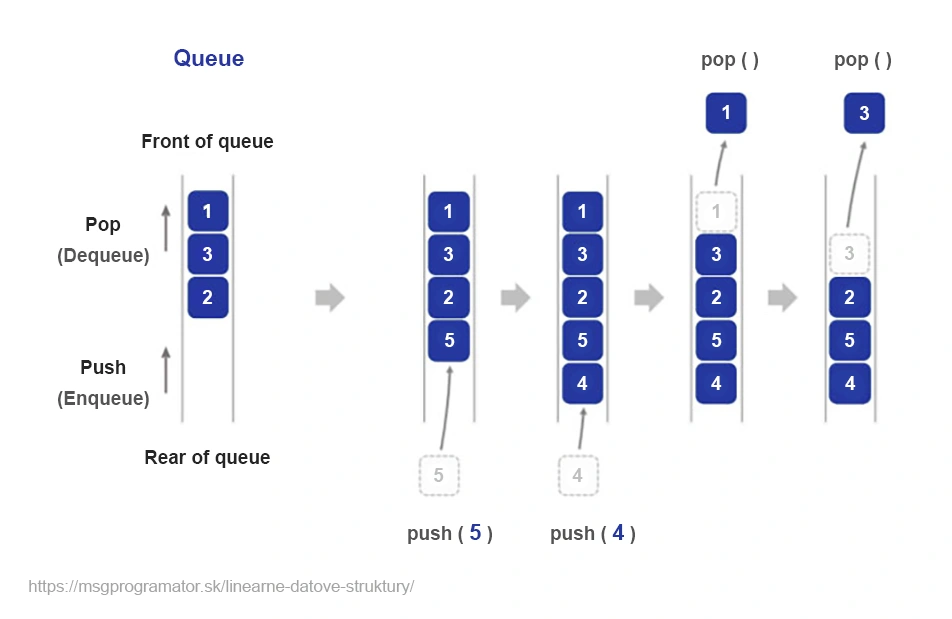
Fronta je základná dátová štruktúra, ktorá funguje na princípe „prvý dovnútra, prvý von“ (FIFO – First In, First Out). Predstaviť si ju môžeme ako poradie objednávok čakajúcich na vybavenie – tá, ktorá prišla ako prvá bude aj ako prvá vybavená. Táto štruktúra je mimoriadne užitočná v situáciách, kde je dôležité zachovať poradie spracovania údajov.

Základné vlastnosti fronty

• Operácie na koncoch: Nové prvky sa pridávajú na koniec (enqueue) a odoberajú sa z prednej časti (dequeue), čím sa zachová FIFO správanie.
• Dynamická veľkosť: V závislosti od implementácie môže fronta rásť alebo sa zmenšovať počas behu programu.
• Sekvenčný prístup: Prístup je možný iba k prvku na začiatku (front) alebo na konci (rear) fronty.

Kľúčové operácie fronty

• Enqueue: Pridá prvok na koniec fronty.
  Dequeue: Odstráni a vráti prvok z prednej časti fronty.
  Peek (Front): Zobrazí prvý prvok vo fronte bez jeho odstránenia.
  IsEmpty: Skontroluje, či je fronta prázdna.

Typy front

• Jednoduchá fronta (Queue): Klasická FIFO štruktúra, kde sa prvky pridávajú na koniec a odoberajú zo začiatku.
• Kruhová fronta (Circular Queue): Efektívnejší variant, ktorý opätovne využíva uvoľnený priestor tým, že posledný index sa prepája späť na prvý.
• Prioritná fronta (Priority Queue): Každý prvok má priradenú prioritu a spracúva sa podľa nej, bez ohľadu na poradie pridania.
• Obojsmerná fronta (Deque – Double-Ended Queue): Umožňuje pridávanie a odoberanie prvkov na oboch koncoch.

Výhody použitia fronty

• Zachovanie poradia: Ideálna na aplikácie, kde je dôležité spracúvať prvky v poradí ich príchodu.
• Efektivita: Pridávanie a odoberanie prvkov je časovo efektívne, s časovou zložitosťou O(1) v prípade správnej implementácie (napr. kruhovej fronty).
• Jednoduchosť: Koncept fronty je jednoduchý na pochopenie a implementáciu.

Nevýhody použitia fronty

• Obmedzený prístup: Možno manipulovať iba s prvým a posledným prvkom, čo ju robí nevhodnou pre úlohy vyžadujúce náhodný prístup.
• Pamäťová neefektivita: Pri implementácii pomocou polí môže byť jednoduchá fronta neefektívna, ak sa uvoľnený priestor nerecykluje.

Použitie fronty

• Správa procesov: Operačné systémy používajú fronty na plánovanie procesov, kde úlohy čakajú na vykonanie v poradí ich príchodu.
• Spracovanie dátových tokov: V sieťovej komunikácii a streamovaní videa sa fronty používajú na riadenie príjmu a spracovania dát.
• Šírkové prehľadávanie grafov: Pri algoritmoch, ako je Breadth-First Search (BFS), fronty zabezpečujú postupné prehľadávanie susedných vrcholov grafu.
• Obsluha požiadaviek: Webové servery alebo databázy používajú fronty na spracovanie prichádzajúcich požiadaviek (HTTP requests) podľa poradia ich prijatia.

Príklad použitia

Predstavme si pokladňu v supermarkete. Každý zákazník, ktorý príde, sa zaradí na koniec radu (enqueue). Pokladník obslúži vždy zákazníka na začiatku radu (dequeue). Tento proces zachováva poradie príchodu zákazníkov.

Fronty sú užitočné všade tam, kde je potrebné efektívne spracovávať úlohy alebo údaje v poradí ich príchodu. Napriek obmedzeniam svojho sekvenčného prístupu sú jednou z najdôležitejších štruktúr v oblasti programovania.

Nelineárne dátové štruktúry

Teraz si podrobne rozoberieme nelineárne dátové štruktúry, ich základne vlastnosti, typy, výhody a nevýhody, ako aj najčastejšie prípady/príklady použitia.

Strom (Tree)

Strom je základná nelineárna dátová štruktúra, ktorá organizuje dáta hierarchicky. Skladá sa z uzlov, kde každý uzol má jeden nadradený uzol – rodiča (okrem koreňového uzla) a môže mať nula alebo viacero podriadených uzlov – potomkov. Táto štruktúra umožňuje efektívne spracovanie údajov, najmä pri hľadaní, triedení a reprezentácii vzťahov.

Základné vlastnosti stromu

Hierarchická štruktúra: Stromy sú usporiadané do hierarchických vrstiev, pričom koreň je na vrchole a uzly pod ním reprezentujú ďalšie úrovne.

Uzly a hrany: Každý uzol obsahuje dáta a odkazy na svoje podriadené uzly. Hrany reprezentujú spojenia medzi uzlami.

Koreň (root): Je najvyšší uzol stromu, ktorý nemá rodičovský uzol.

Listy: Sú uzly, ktoré nemajú žiadnych potomkov (známe aj ako koncové uzly).

Výška stromu: Počet hrán na najdlhšej ceste od koreňa k listu.

Typy stromov

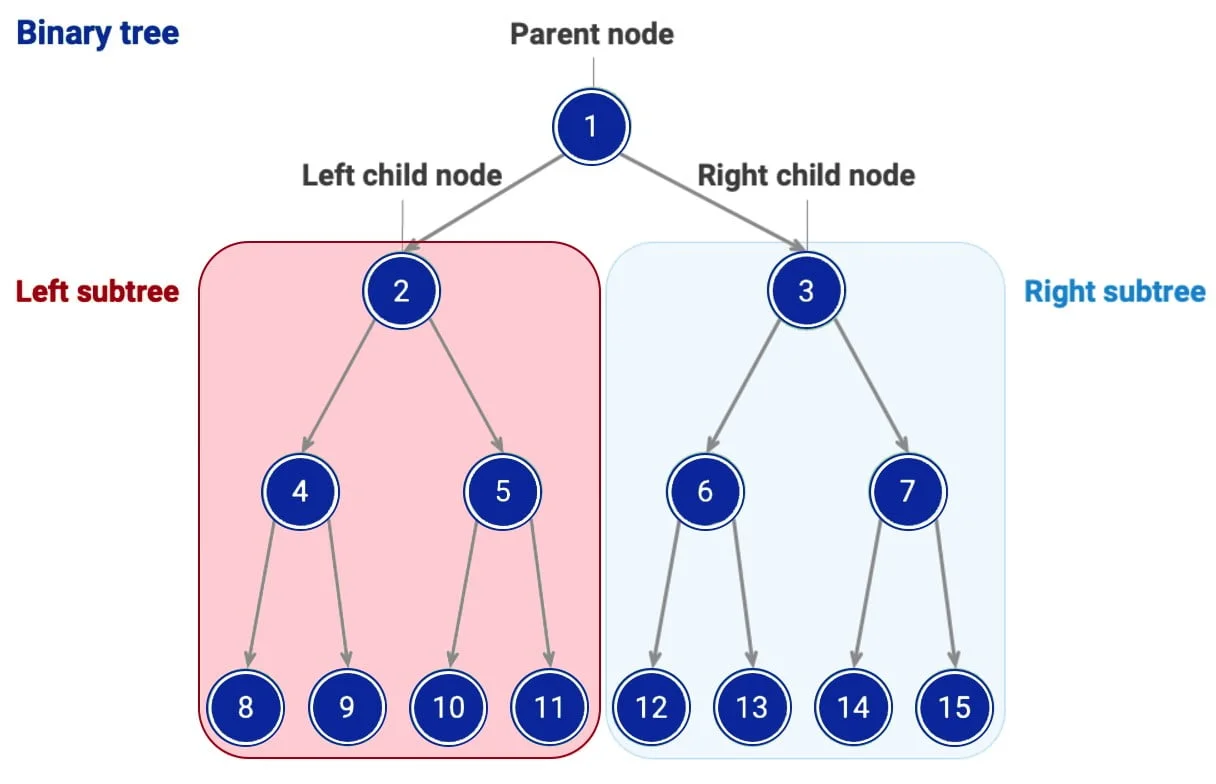
Binárny strom: Každý uzol môže mať najviac dvoch potomkov – ľavý a pravý uzol.

Binárny vyhľadávací strom (BST): Binárny strom, kde ľavé podstromy obsahujú hodnoty menšie ako uzol a pravé podstromy hodnoty väčšie.

Vyvážené stromy: Stromy, ako AVL alebo červeno-čierne stromy, ktoré udržiavajú vyváženú výšku pre efektívnejšie operácie.

N-árny strom: Uzly môžu mať až N podriadených uzlov.

Trie: Špecializovaný strom na efektívne vyhľadávanie, napríklad pri práci so slovami alebo prefixmi.

Výhody použitia stromu

• Efektívne vyhľadávanie a triedenie: Stromy, najmä binárne vyhľadávacie stromy, umožňujú rýchle vyhľadávanie a usporiadanie dát.
• Flexibilita reprezentácie: Umožňujú modelovať hierarchické vzťahy, ako organizačné štruktúry, súborové systémy alebo taxonómiu.
• Dynamická povaha: Stromy môžu rásť alebo sa zmenšovať bez pevne stanovenej veľkosti.

Nevýhody použitia stromu

• Zložitejšia implementácia: Práca so stromami vyžaduje správu ukazovateľov na uzly stromov, čo môže byť náchylné na chyby.
• Pamäťová náročnosť: Každý uzol potrebuje dodatočnú pamäť na odkazy na svoje podriadené uzly.
• Neefektívnosť pri nevyvážených stromoch: Stromy, ktoré nie sú vyvážené, môžu degradovať na lineárnu štruktúru, čo vedie k zhoršeniu výkonu na O(n).

Použitie stromov

• Databázové indexy: B-stromy a ich varianty sa používajú na efektívne vyhľadávanie a správu veľkých množín dát.
• Súborové systémy: Stromy reprezentujú štruktúru priečinkov a súborov na disku.
• Hľadanie ciest v grafoch: Stromy sú základom algoritmov na hľadanie ciest alebo pokrytie grafov.
• Kompresia dát: Huffmanove stromy sú používané pri algoritmoch na kompresiu, ako je zip alebo gzip.

Príklad použitia

Predstavte si rodokmeň – koreň stromu predstavuje najstaršieho predka a uzly nižšie znázorňujú jeho potomkov. Táto hierarchia je priamym príkladom využitia stromu na organizáciu a prehľadnú reprezentáciu údajov.

Stromy sú jednou z najdôležitejších dátových štruktúr v informatike. Ich schopnosť modelovať zložité vzťahy a efektívne manipulovať s hierarchickými dátami z nich robí neoddeliteľnú súčasť moderných algoritmov a aplikácií.

Graf (Graph)

Graf je nelineárna dátová štruktúra, ktorá reprezentuje objekty (uzly, nazývané vrcholy) a vzťahy medzi nimi (nazývané hrany). Táto štruktúra je mimoriadne univerzálna a používa sa na modelovanie rôznych situácií, ako sú sociálne siete, dopravné mapy alebo vzťahy medzi entitami v databázach.

Základné vlastnosti grafu

Vrcholy (Nodes): Základné časti grafu, ktoré reprezentujú objekty alebo entity.

Hrany (Edges): Spojenia medzi vrcholmi, ktoré reprezentujú vzťahy alebo interakcie.

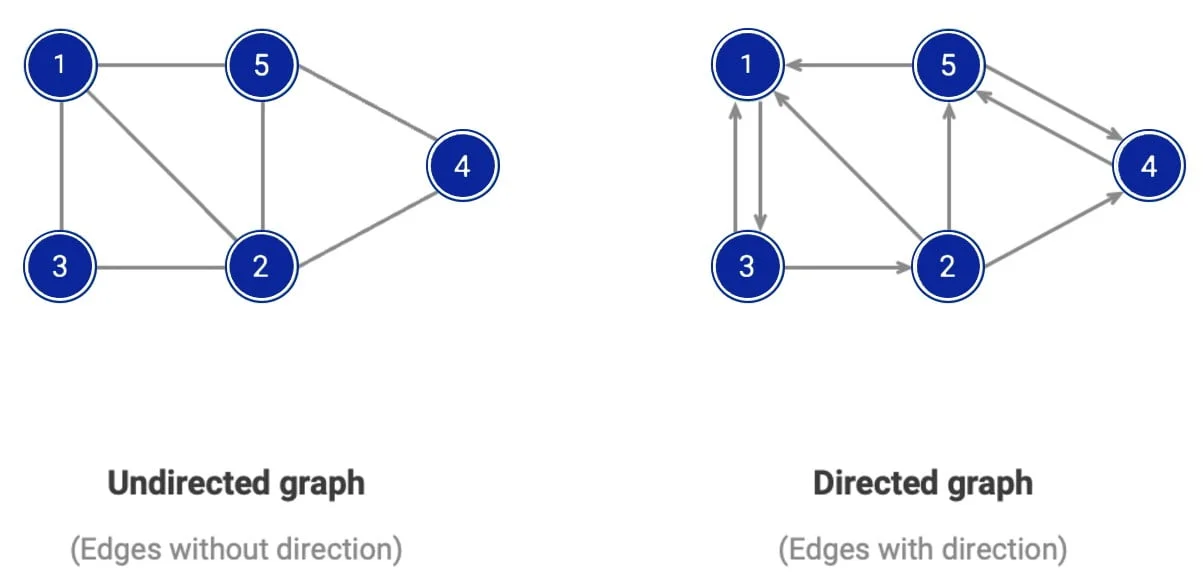
Orientácia: Graf môže byť orientovaný (smerované hrany, napr. jednosmerná ulica) alebo neorientovaný (bez smerovania, napr. obojsmerná cesta).

Váha hrán: Niektoré grafy obsahujú váhy na hranách, ktoré reprezentujú hodnoty ako vzdialenosti, náklady alebo čas.

Typy grafov

Neorientovaný graf (Undirected Graph): Hrany nemajú smer, spojenie medzi dvoma vrcholmi je vzájomné.

Orientovaný graf (Directed Graph alebo Digraph): Hrany majú smer a spájajú vrcholy v určitom poradí.

Vážený graf (Weighted Graph): Hrany majú pridelenú hodnotu (váhu).

Cyklový graf (Cyclic Graph): Obsahuje uzavreté cesty (cykly).

Acyklický graf (Acyclic Graph): Neobsahuje žiadne cykly.

Strom (Tree Graph alebo Tree): Špeciálny prípad acyklického grafu, kde je každý vrchol prístupný cez jednu cestu.

Súvislý graf (Connected Graph): Medzi každými dvoma vrcholmi existuje cesta.

Výhody použitia grafov

• Flexibilita reprezentácie: Grafy sú vhodné na modelovanie akýchkoľvek vzťahov, od sieťových topológií po interakcie medzi ľuďmi.
• Efektívne vyhľadávanie: Množstvo algoritmov je optimalizovaných na prácu s grafmi, ako je Dijkstrov algoritmus na hľadanie najkratšej cesty.
• Možnosť vizualizácie: Grafy sú intuitívne na pochopenie a vizuálnu interpretáciu, čo zjednodušuje analýzu dát.

Nevýhody použitia grafov

• Pamäťová náročnosť: Ukladanie veľkých grafov, najmä ak sú husté, môže byť veľmi pamäťovo náročné.
• Zložitosť operácií: Implementácia a správa grafov môže byť zložitá, najmä pri dynamických zmenách.
• Potenciálna neefektivita: Niektoré algoritmy na grafy majú vysokú časovú zložitosť, čo môže byť problematické pre veľké grafy.

Použitie grafov

• Sociálne siete: Modelovanie vzťahov medzi používateľmi, ako sú priateľstvá alebo sledovania.
• Navigácia a doprava: Reprezentácia ciest, železníc alebo leteckých trás.
• Optimalizácia procesov: Hľadanie najefektívnejšej cesty, minimálneho nákladového stromu alebo maximálneho prietoku.
• Webové prehľadávače: Vyhľadávače používajú grafy na indexovanie a analýzu spojení medzi webovými stránkami.
• Biológia a chemické štruktúry: Reprezentácia molekúl, génových sietí alebo evolučných vzťahov.

Príklad použitia

Predstavme si mestskú dopravnú sieť. Každé miesto (zastávka) je vrchol a spojenie medzi zastávkami je hrana. Ak chceme nájsť najrýchlejšiu cestu medzi dvoma miestami, použijeme algoritmus, ktorý prechádza graf a identifikuje najkratšiu trasu.

Grafy sú nenahraditeľné pri riešení komplexných problémov, kde je kľúčové pochopiť a vedieť analyzovať vzťahy medzi objektmi. Vďaka svojej všestrannosti a bohatým možnostiam ich aplikovania sa stali základom mnohých oblastí modernej informatiky.

Tabuľkové dátové štruktúry

Teraz si podrobne rozoberieme tabuľkové dátové štruktúry, ich základne vlastnosti, typy, výhody a nevýhody, ako aj najčastejšie prípady/príklady použitia.

Hašovacia tabuľka (Hash Table)

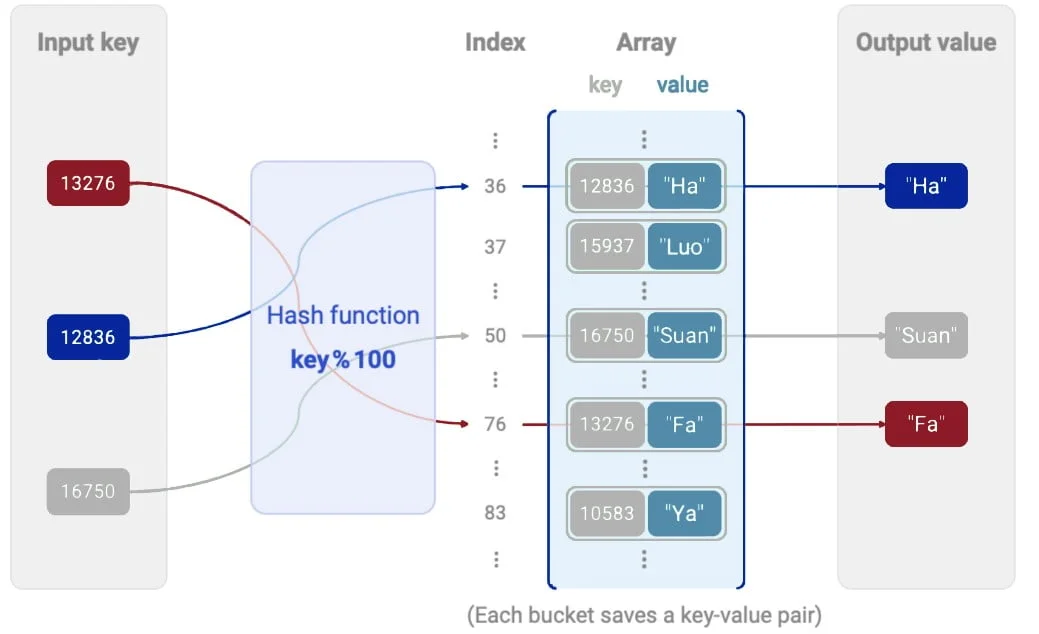
Hašovacia tabuľka je dátová štruktúra, ktorá implementuje asociatívne pole, v ktorom sa hodnoty (dáta) ukladajú a vyhľadávajú na základe unikátneho kľúča. Používa hašovaciu funkciu, ktorá prevádza kľúč na index v poli, čím umožňuje efektívne ukladanie a prístup k údajom.

Základné vlastnosti hašovacej tabuľky

Hašovacia funkcia: Kľúč sa pomocou tejto funkcie prevádza na index v príslušnom poli. Kvalita hašovacej funkcie určuje výkon tabuľky.

Unikátne kľúče: Každý záznam v tabuľke je priradený unikátnemu kľúču.

Kolízie: Ak dva rôzne kľúče generujú rovnaký index, dochádza ku kolízii, ktorá sa rieši špecifickými technikami (napr. separátnym reťazením).

Riešenie kolízií

Separátne reťazenie: Každý index v tabuľke obsahuje zoznam alebo inú štruktúru, do ktorej sa ukladajú všetky hodnoty s rovnakým indexom.

Otvorené adresovanie: Ak nastane kolízia, hľadá sa iný voľný slot podľa určitého vzoru (napr. lineárne alebo kvadratické sondovanie).

Výhody použitia hašovacej tabuľky

• Rýchlosť operácií: V ideálnom prípade majú operácie vyhľadávania, vkladania a mazania časovú zložitosť O(1).
• Efektívne využitie pamäte: Tabuľka dynamicky spravuje priestor podľa počtu uložených prvkov.
• Jednoduchý prístup k údajom: Umožňuje efektívne párovanie a rýchle vyhľadávanie na základe kľúčov.

Nevýhody použitia hašovacej tabuľky

• Závislosť od hašovacej funkcie: Slabá funkcia môže viesť k častým kolíziám a znížiť výkon.
• Pamäťová náročnosť: Pri vysokom počte kľúčov môže byť potrebné veľké množstvo pamäte.
• Neusporiadané dáta: Tabuľka nezachováva poradie záznamov, čo môže byť nevýhodné pri niektorých aplikáciách.

Použitie hašovacej tabuľky

• Rýchle vyhľadávanie: Používa sa na implementáciu máp, slovníkov a asociatívnych polí vo väčšine programovacích jazykov.
• Caching: Tabuľky sú základom vyrovnávacích pamätí, kde je rýchly prístup ku často používaným údajom kľúčový.
• Detekcia duplicít: Rýchlo zistí, či určitý prvok už existuje, čo je užitočné napríklad pri filtroch, ako je Bloomov filter.
• Databázové indexy: Používa sa na optimalizáciu prístupu k údajom v databázach.
• Šifrovanie: Hašovacie funkcie sú kľúčové pri generovaní unikátnych kontrolných súčtov.

Príklad použitia

Predstavme si telefónny zoznam, v ktorom chceme rýchlo vyhľadať číslo osoby na základe jej mena. Meno osoby slúži ako kľúč, ktorý sa pomocou hašovacej funkcie prevedie na index. Na tomto indexe je uložené príslušné telefónne číslo.

Hašovacie tabuľky sú výkonnou a efektívnou štruktúrou pre širokú škálu aplikácií, kde je prioritou rýchly prístup k údajom. Ich schopnosť efektívne spracovávať veľké množstvá dát ich robí nenahraditeľnými v celej oblasti IT.

Ďalšie dátové štruktúry

Ešte by som rád stručne spomenul aspoň niektoré menej známe dátové štruktúry, s ktorými sa môžeme v IT stretnúť.

Heap (Halda)

Binárny strom, ktorý spĺňa nasledovnú podmienku (každý rodičovský uzol je väčší alebo menší ako jeho potomkovia). Používa sa na implementáciu prioritných radov alebo v algoritme Heap Sort, ktorý sme si na našom blogu už predstavili.

Trie (Prefixový strom)

Trie je stromová tabuľková štruktúra optimalizovaná na vyhľadávanie reťazcov, kde každý uzol reprezentuje časť kľúča. Používa sa v textových procesoroch, automatickom dopĺňaní alebo pri vyhľadávaní v databázach.

Disjoint Set

Slúži na reprezentáciu a spravovanie množín s disjunktnými prvkami. Používa sa pri grafových algoritmoch, ako je Kruskalov algoritmus.

Segment Tree (Intervalový strom)

Strom navrhnutý na efektívne riešenie problémov spojených s intervalmi a rozsahmi údajov. Je vhodný pre rýchle operácie na určenie sumy, minima alebo maxima v rozsahu.

Fenwick Tree

Efektívna štruktúra na aktualizáciu a vyhľadávanie súčtov v postupnostiach. Používa sa v úlohách, ktoré počítajú rozsahy.

K-D Tree (K-Dimenzionálny strom)

Špecializovaný strom na organizáciu bodov v K-rozmernom priestore. Využíva sa v algoritmoch pre spracovanie obrazu, počítačové videnie a databázové vyhľadávanie.

Suffix Tree

Reprezentuje všetky sufixy daného reťazca. Efektívny je najmä pri hľadaní podreťazcov a textových algoritmoch.

Matrix Table (Maticová tabuľka)

Maticové tabuľky sú dvojrozmerné alebo viacrozmerné polia, ktoré ukladajú dáta v riadkoch a stĺpcoch. Používa sa napr. v lineárnej algebre pre prácu s maticami.

Adjacency Matrix (Matica susedností)

Dvojrozmerná matica, kde riadky a stĺpce reprezentujú vrcholy grafu a hodnoty v matici indikujú existenciu hrán medzi vrcholmi. Používa sa na efektívne reprezentovanie hustých grafov a na rýchle zisťovanie existencie hrany medzi dvoma vrcholmi.

Adjacency List  (Zoznam susedností)

Zoznam, kde každý vrchol grafu obsahuje zoznam všetkých svojich susedných vrcholov. Ideálny na reprezentáciu riedkych grafov, pretože šetrí pamäť v porovnaní s maticou susednosti.

Sparse Matrix (Riedka matica)

Štruktúra na ukladanie matíc s väčšinou nulových hodnôt, kde sa ukladajú iba nenulové hodnoty a ich polohy. Používa sa v oblastiach, ako je strojové učenie, analýza grafov a modelovanie veľkých riedkych dátových štruktúr.

Scatter Table (Rozptylová tabuľka)

Tabuľková štruktúra podobná hašovacej tabuľke, ktorá rieši kolízie alternatívnym spôsobom rozptyľovania kľúčov.  Efektívna na spracovanie veľkého objemu dát s nižším rizikom zhlukovania pri kolíziách v hašovacích štruktúrach.

Záver

Dátové štruktúry sú neodmysliteľnou súčasťou programovania, pretože poskytujú spôsob ako efektívne organizovať, spracovať a manipulovať údaje. Lineárne dátové štruktúry (queue, stack, linked list, array) majú svoje špecifické výhody, nevýhody a oblasti použitia.

Ich správny výber a implementácia môže významne ovplyvniť výkon a efektivitu softvéru. Preto je pochopenie základných princípov dátových štruktúr kľúčové pre každého, kto sa chce hlbšie venovať programovaniu, algoritmom alebo databázam, aby tieto znalosti mohol využiť pri tvorbe optimalizovaných a inovatívnych riešení.

Ak hľadáš prácu a si Java programátor, prezri si naše benefity pre zamestnancov a reaguj na najnovšie ponuky práce.