Bubble sort algorithm Java
Sorting algorithms are used to reorder the elements of an array or list in ascending or descending numerical or lexicographic order. Data sorting is very important for the optimal performance of other algorithms that require sorted input data.

There are a number of different sorting algorithms. The selection of an appropriate algorithm depends on factors such as the size and characteristics of the input data, available memory, and time and space requirements.
To make your choice easier, in our series we will introduce the most well-known data sorting algorithms, explain their principles, advantages and disadvantages, and program them in Java.
Today we will look at bubble sort.
Bubble algorithm
Bubble sort is a sorting algorithm that compares every two adjacent elements in turn and swaps them until they are sorted in the desired order. The algorithm requires multiple iterations.
The name of the algorithm is derived from the air bubbles that rise to the surface in water. Analogously in the algorithm, the elements of the array bubble up in each iteration to the end of the unsorted portion of the array.
Bubble sort algorithm working principle
Suppose we want to sort the elements in ascending order. If an array has only one element, it is considered sorted, otherwise the elements need to be sorted.
First iteration:
All two adjacent array elements are compared sequentially from the beginning of the array. If the first element is larger than the second, they swap places. Then the second element is compared with the third, the third with the fourth, and so on. The first iteration ends by comparing the last adjacent elements.
During the first iteration, swapping elements is guaranteed to get the largest element of the array to the end of the array.
Other iterations:
The last index of the array is considered sorted, the rest of the array is not sorted yet. For the unsorted part of the array, the procedure from the first iteration is repeated. Each iteration bubbles the largest element to the end of the unsorted portion of the array. This is repeated until the array is sorted.
Number of iterations: n-1
Number of comparisons: n*(n-1)/2
Example
We have the following array of elements [3][1][2]. From the formulas, we can calculate that the number of required iterations is 2, and the number of comparisons is 6.
In the first iteration, the following operations take place: [1][3][2] -> [1][2][3]. The largest element 3 was moved to the last index of the array. Even though the array is already sorted, a second iteration is performed which compares the first two elements of the array, and since the first and second elements have the correct order, there is no swapping of their order.
Optimizing bubble sort algorithm
In the example mentioned above, we saw that even if the array is already sorted, unnecessary additional iterations and comparisons are performed. This of course increases the running time of the algorithm. The solution is to note at each iteration whether there is a change in the order of any two elements. If not, we consider the array to be sorted and do not perform subsequent iterations. This optimization will reduce the time complexity for the already sorted array and ensure the adaptivity of the algorithm.
Bubble sort advantages
- It is easy to understand and implement
- Does not require additional memory when sorting
- It is stable, that is, two identical elements from the input retain their relative order in the result
Bubble sort disadvantages
- The time complexity is O(n²), which makes it a slow algorithm for a large dataset
Bubble sort time consumption
| Algorithm | Method | Time complexity | Memory | Stable | ||
| worst | average | best | ||||
| Bubble sort | exchange | O(n²) | O(n²) | O(n) | O(1) | Yes |
Bubble sort animation, visualization, gif
The visualization of the Bubble sort algorithm looks like this:
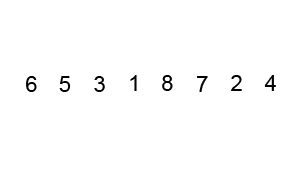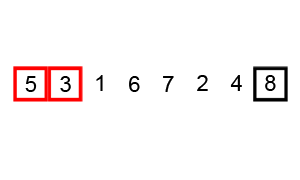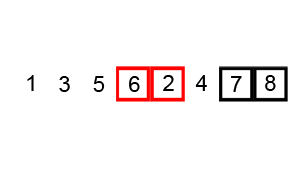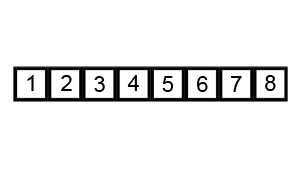
V článku sa dozvieš:
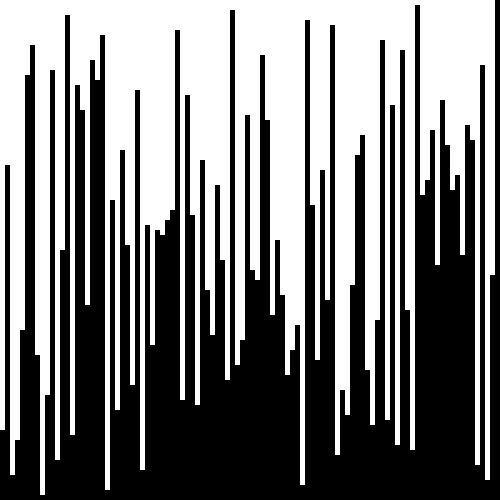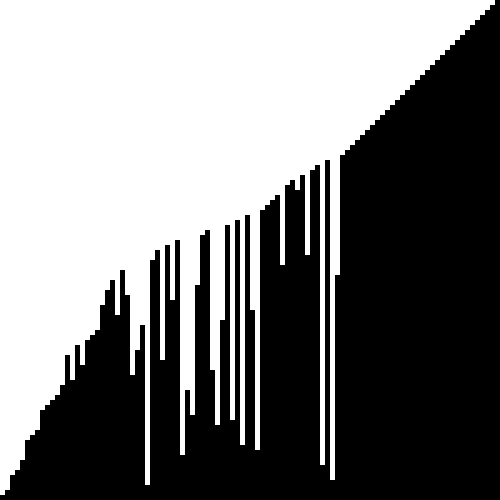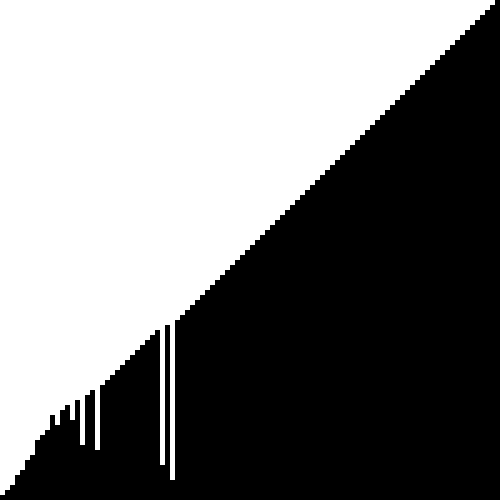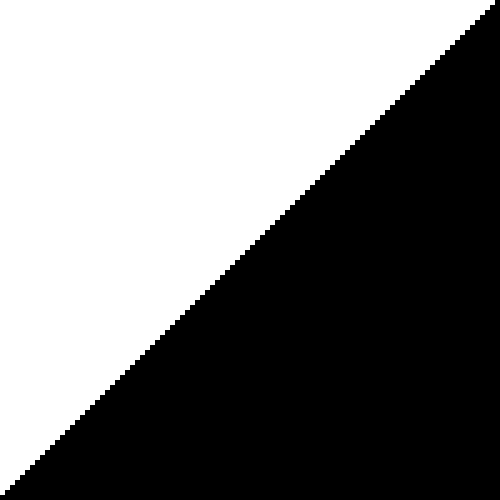
Source: commons.wikimedia.org/wiki/Category:Animations_of_sort_algorithms
An animation of the algorithm can be found on Toptal. There are 8 types of algorithms, you can also play the animation backwards.
On this page you can go through the steps of the algorithm to check the time consumption of the algorithm.
Bubble Sort Implementation – Java example
Let’s program an optimized version of bubble sort in Java.
BubbleSort.java
package sorting;
// An optimized version of Bubble Sort
public class BubbleSort {
private boolean change;
private int temp;
public void sort(int data[])
{
for (int i = 0; i < data.length - 1; i++) {
System.out.println(i + 1 + ". iteration");
change = false;
for (int j = 0; j < data.length - i - 1; j++) {
if (data[j] > data[j + 1]) {
// Swap arr[j] and arr[j+1]
temp = data[j];
data[j] = data[j + 1];
data[j + 1] = temp;
change = true;
printArray(data);
}
}
// If no two elements swapped, then end the sort method
if (!change)
return;
}
}
// Function to print an array
public void printArray(int data[])
{
for (int i = 0; i < data.length; i++)
System.out.print(data[i] + " ");
System.out.println();
}
}Main.java
import sorting.BubbleSort;
public class Main {
public static void main(String[] args) {
int dataToSort[] = { 6, 5, 4, 2, 3, 1, 7 };
BubbleSort bubbleSort = new BubbleSort();
System.out.print("Input: ");
bubbleSort.printArray(dataToSort);
bubbleSort.sort(dataToSort);
System.out.print("Sorted: ");
bubbleSort.printArray(dataToSort);
}
}The output of this example is:

We have prepared the files with the above example in the form of code that you can run directly in Java. Download the BubbleSort code in Java here.
If you’re a Java developer looking for a job, check out our employee benefits and respond to our job offers!


