Java Entwickler Experte
Datenstrukturen: Merkmale und Typen
In der heutigen digitalen Welt sind Daten zu einer der wertvollsten Ressourcen geworden. Egal ob es sich um soziale Netzwerke handelt, die täglich Milliarden von Interaktionen zwischen Menschen im virtuellen Raum des Internets analysieren, um Gesundheitssysteme, die Informationen über Patienten und Krankheiten speichern, die einen Arzt aufsuchen, oder um digitale Handelsinstrumente wie Bitcoin, der gerade die magische Grenze von 100.000 Dollar pro Bitcoin erreicht.
In diesem Artikel erfährst du:
Daten sind allgegenwärtig und treiben Innovationen in allen Bereichen menschlicher Aktivität voran. Ihre effektive Nutzung erfordert jedoch ein Verständnis ihrer Struktur und Verarbeitung – und genau hier kommen die Datenstrukturen ins Spiel. Daten an sich wären nutzlos, wenn wir nicht wüssten, wie wir sie effizient organisieren, speichern und verarbeiten können.
Stellen wir uns eine Bibliothek ohne jegliches System zur Ordnung der Bücher vor – ein Chaos, in dem es nahezu unmöglich ist, das Gesuchte zu finden. Ähnlich wäre die Welt der Computersysteme nicht in der Lage, das heutige Datenvolumen zu bewältigen, ohne durchdachte und optimierte Datenstrukturen.
Diese Strukturen, die für uns Nutzer eine unsichtbare Architektur darstellen, sind verantwortlich für die korrekte Kategorisierung, Speicherung und Verarbeitung von Daten, sodass z. B. die Sekretärin, die mit Bürosoftware arbeitet, der Spieler eines aktuellen Computerspiels, der Kunde, der während des Black Friday im Online-Shop einkauft, oder der Programmierer, der Abfragen in einer großen Datenbank durchführt, erhielten fast sofort genau die Daten, die sie im jeweiligen Moment benötigten oder erwarteten.
In diesem Artikel tauchen wir in die faszinierende Welt der Datenstrukturen ein. Wir werden uns mit den grundlegenden Strukturen wie Arrays und Listen befassen. Von den grundlegenden wie Arrays und Listen bis hin zu fortgeschrittenen wie Hash-Tabellen oder Binärbäumen zeigen wir, wie jede von ihnen eine Schlüsselrolle bei der Lösung verschiedener Berechnungsprobleme spielt. Du wirst erfahren, warum einige Datenstrukturen ideal für schnelles Suchen, andere für das Speichern großer Datenmengen und wieder andere für die dynamische Verwaltung von Daten geeignet sind.
Egal, ob du ein Anfänger in der Programmierung bist, ein neugieriger Informatikstudent, der die Grundlagen seines zukünftigen Handwerks besser verstehen möchte, oder bereits in der IT-Branche arbeitest, dieser Artikel bietet dir einen praktischen Einblick in die Bedeutung der richtigen Auswahl von Datenstrukturen.
Das Missverstehen der Schlüsselfunktionen, Stärken und Schwächen einer bestimmten Datenstruktur und ihre ungeeignete, ineffiziente Verwendung führt nicht nur zu wertvoller verlorener Verarbeitungszeit, sondern verschwendet auch Hardware-Ressourcen. Wie wir alle wissen, Zeit ist Geld, und zum Beispiel Langsame Reaktionszeiten bei der Produktsuche in einem Online-Shop (d.h. die Verarbeitung und Filterung von Daten basierend auf den vom Nutzer angegebenen Kriterien) haben bereits viele Kunden vom Kauf abgehalten.
Daten sind nicht nur bedeutungslose binäre Zahlen oder Text, der aus seltsamen ASCII-Zeichen besteht – sie sind die Grundlage unseres Lebens. Die Welt der modernen Technologien wird von Daten, effizienten Datenstrukturen und Algorithmen angetrieben, und dieser Artikel stellt dir einige davon vor.
Was sind Daten?
Daten sind die Bausteine von Informationen. Sie sind gewöhnliche Fakten, Zahlen, Texte, Symbole, Klänge oder Bilder, die ohne Kontext keine konkrete Bedeutung haben. Wir können sie uns wie einzelne Teile eines Puzzles vorstellen – einzeln sind sie nur kleine Teile eines Ganzen, aber wenn sie richtig angeordnet sind, können sie ein schönes Bild ergeben oder die solide Grundlage für etwas Größeres werden.
Merkmale der Daten
- Grobheit: Die Daten sind uninterpretiert. Die Zahl „42“ zum Beispiel sagt für sich genommen nicht viel aus – sie könnte ein Alter, die Anzahl der Seiten in einem Buch oder einfach eine zufällige Zahl sein.
- Potenzial für Informationen: Wenn Daten verarbeitet, analysiert oder in einen Kontext gestellt werden, werden sie in Informationen umgewandelt. Zum Beispiel bedeutet „42 °C“ im Zusammenhang mit dem Wetter extreme Hitze.
- Digitale Darstellung: In der modernen Informatik werden Daten digital repräsentiert – in Form von binären Werten (0 und 1), die die Grundlage der Computeroperationen bilden.
Kategorien von Daten
Wir können die Daten auf der Grundlage der Strukturierung wie folgt unterteilen:
- Strukturierte Daten – Daten, die in einer organisierten Form gespeichert sind, z.B. in Tabellen oder Datenbanken, in denen einzelne Werte bestimmten Attributen zugewiesen sind.
- Unstrukturierte Daten – Textdokumente, Bilder, Videos oder Audioaufnahmen, die keine vordefinierte Struktur haben.
- Halbstrukturierte Daten – Daten, die eine gewisse organisatorische Struktur aufweisen, wie z. B. XML- oder JSON-Dateien, aber nicht so streng strukturiert sind wie Tabellen.
Die Bedeutung von Daten
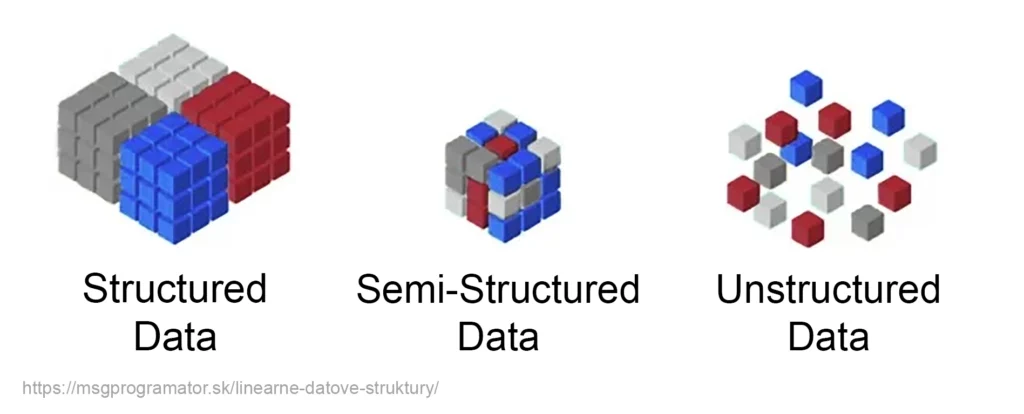
Daten bilden die Grundlage für alle Entscheidungen in der modernen Welt. Unternehmen nutzen sie für Marktanalysen, Wissenschaftler für die Forschung, Ärzte für die Diagnose und Behandlung und Regierungen für die Haushaltsplanung. Künstliche Intelligenz (KI), wie wir sie heute kennen, wäre ohne sie nicht möglich gewesen. Dank der Technologien, die die Erfassung, Verarbeitung und Analyse riesiger Datenmengen ermöglichen, können wir heute Muster aufdecken, Vorhersagen treffen und Statistiken nutzen, um neue Erkenntnisse zu gewinnen, die uns sonst verborgen bleiben würden.
Datenstrukturen
Datenstrukturen stellen eine Möglichkeit dar, Daten zu organisieren, zu speichern und zu verarbeiten, damit sie in Computerprogrammen effizient genutzt werden können. Sie geben den Daten eine bestimmte Form und bestimmen, wie die Daten angeordnet werden, aber auch, wie sie manipuliert werden können. Sie sind die Grundbausteine eines Programms.
Entwurfsprinzipien für Datenstrukturen
Beim Entwurf einer Datenstruktur oder bei der Auswahl einer bestehenden Struktur versuchen wir immer, die Geschwindigkeit von Vorgängen wie Datensuche, -abruf und -schreibung zu optimieren. Eine zweite Sache, die Sie im Auge behalten sollten, ist, dass effiziente Datenstrukturen den Speicherplatzbedarf minimieren sollten. Dazu gehört nicht nur der Speicherplatz für die Daten, sondern auch Hilfsstrukturen, Indizes oder Metadaten, die ein schnelleres Auffinden der aktuell angeforderten Informationen ermöglichen. Die Implementierung der Datenstruktur sollte für die betreffenden Daten so einfach wie möglich sein, um das Risiko von Fehlern auszuschließen. Außerdem ist es wichtig, die Datenstruktur so zu gestalten, dass sie flexibel und für verschiedene Anwendungen leicht erweiterbar ist.
Die effiziente Auswahl und Implementierung von Datenstrukturen hat einen großen Einfluss auf die Komplexität der Algorithmen, die sie verwenden, und damit auf die Gesamtleistung der Anwendung.
Arten von Datenstrukturen
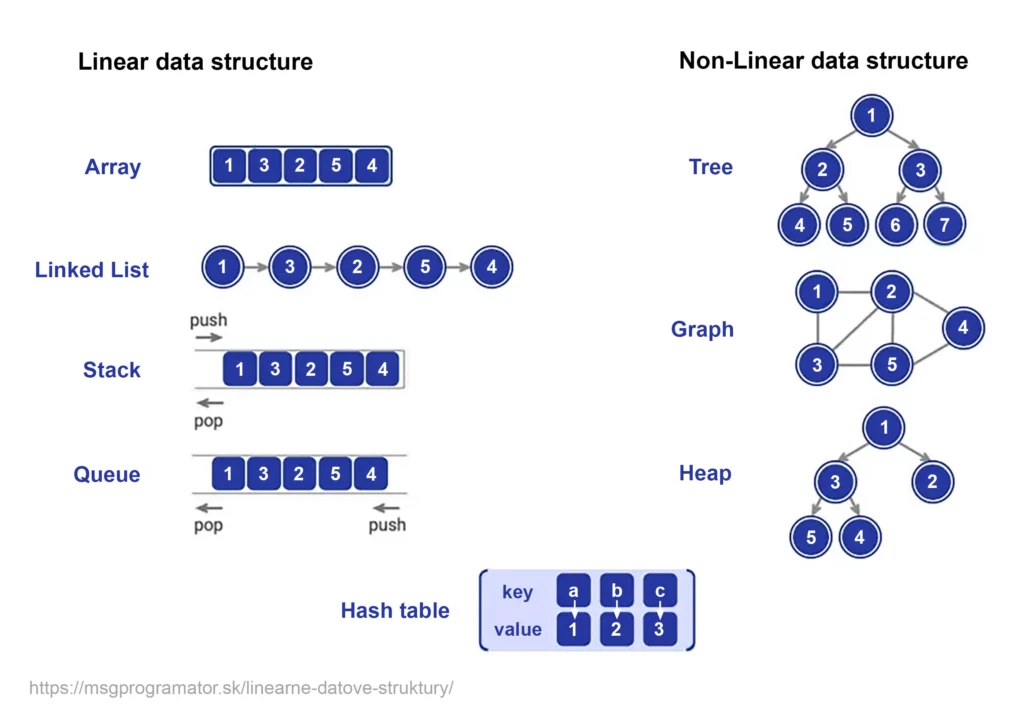
Datenstrukturen können nach ihrer Architektur der Datenspeicherung in folgende Kategorien unterteilt werden:
- Lineare Datenstrukturen
In einer linearen Datenstruktur sind alle Elemente in einer linearen oder sequentiellen Reihenfolge angeordnet. Typische Beispiele für diese Art von Struktur sind: Feld (array), verkettete Liste (linked list), Stapel( stack) und Warteschlange (queue).
Nichtlineare DatenstrukturenIn einer nichtlinearen Datenstruktur sind die Elemente hierarchisch oder in einer mehrstufigen komplexen Datenstruktur angeordnet. Typische Beispiele für diese Art von Struktur sind: Baum (tree) undGraph (graph).- Tabellarische Datenstrukturen
Dazu gehören Datenstrukturen, die nach dem Prinzip der Hash-Tabelle arbeiten.
Grundlegende Operationen mit Datenstrukturen
Suche – jedes Element in der Datenstruktur kann durchsucht werden.
Einfügen – Einfügen eines neuen Elements in die Datenstruktur.
Aktualisieren – Ersetzen eines Elements durch ein anderes Element in der Datenstruktur.
Löschen – Entfernen eines vorhandenen Elements aus der Datenstruktur.
Sortieren – Elemente der Datenstruktur können entweder aufsteigend oder absteigend sortiert werden. In unseren früheren Artikeln haben wir die Datensortierung und Sortieralgorithmen ausführlich behandelt.
Abstrakter Datentyp vs. Datenstruktur
Eine Datenstruktur wird manchmal mit einem abstrakten Datentyp (ADT) verwechselt.
Die ADT sagt, was zu tun ist, und die Datenstruktur sagt, wie es zu tun ist. Mit anderen Worten, wir können sagen, dass die ADT uns das Design liefert, während die Datenstruktur den Implementierungsteil liefert. In einer bestimmten ADT können verschiedene Datenstrukturen implementiert werden. Zum Beispiel. Der ADT-Stack kann auf der Datenebene eine Array- oder Linked-List-Datenstruktur verwenden. Die Entscheidung, was verwendet werden soll, liegt beim Programmierer und seinen spezifischen Anforderungen.
Lineare Datenstrukturen
Wir werden nun im Detail auf lineare Datenstrukturen, ihre grundlegenden Eigenschaften, Typen, Vor- und Nachteile sowie die häufigsten Anwendungsfälle/Beispiele eingehen.
Array (Array)
In der Programmierung sind Arrays eine der teuersten und am häufigsten verwendeten Datenstrukturen. Sie speichern Elemente in einem zusammenhängenden Speicherblock, wobei jedes Element über einen numerischen Index zugänglich ist. Während Arrays eine Zugriffszeit von O(1) bieten, was für leseintensive Operationen hervorragend ist, kann die Effizienz von Schreiboperationen (Einfügen und Löschen) je nach Position der Operation im Array und der Gesamtgröße des Arrays stark variieren.
Grundlegende Feldeigenschaften
- Feste Größe: Sobald das Feld deklariert ist, ist seine Größe fest und kann während des Laufs nicht mehr geändert werden. Daher müssen wir im Voraus wissen, wie viele Element-Arrays erstellt werden müssen. In Java kann diese Einschränkung jedoch durch die Verwendung der dynamischen ArrayList-Array-Struktur umgangen werden.
- Homogene Elemente: Arrays speichern in der Regel Elemente desselben Datentyps und gewährleisten so die Einheitlichkeit der gespeicherten Daten.
- Kontinuierliche Speicherzuweisung: Die Elemente werden in fortlaufend zugewiesenen Speicherplätzen gespeichert, was einen effizienten Zugriff auf die Elemente mithilfe von Indizes ermöglicht.
Feldtypen
- Eindimensionale Arrays (One-Dimensional arrays) – eine Reihe von Elementen, die in einer Reihe angeordnet sind.
- Mehrdimensionale Arrays (Multidimensional arrays) – Arrays, die ein oder mehrere Arrays als Elemente enthalten. Damit können man eine Datendarstellung in mehreren Dimensionen erstellen. Zum Beispiel. Das 2D-Array wird für Matrizen verwendet.
Vorteile der Nutzung des Feldes
- Direkter Zugriff auf die Elemente: Der direkte Zugriff auf ein beliebiges Element über seinen Index ermöglicht effiziente Lesevorgänge.
- Speichereffizienz: Sie ist sehr effizient bei der Speicherung einer großen Anzahl von Elementen in einer Reihe. Es muss kein zusätzlicher Speicher für Verweise auf andere Elemente wie in einer verknüpften Liste zugewiesen werden.
Nachteile der Nutzung des Feldes
- Feste Größe: Die Größe des statischen Arrays wird zur Kompilierzeit festgelegt, was diese Struktur unflexibel macht.
- Ineffizientes Einfügen und Löschen: insbesondere für Elemente am Anfang oder in der Mitte des Arrays, da dies ein Scrollen der Elemente erfordert.
- Verschwendung von Speicher: Wenn es nicht vollständig genutzt wird, blockiert es unnötigerweise den Speicher.
Verwendung des Feldes
- Speichern von Daten: insbesondere von Daten, die bereits sortiert wurden und im Feld nicht neu sortiert werden.
- Nachschlagetabellen: Arrays können effizient Nachschlagetabellen implementieren, die einen schnellen Zugriff auf vorberechnete Werte ermöglichen.
- Implementierung anderer Datenstrukturen: Das Array ist die Grundstruktur für komplexere Datenstrukturen wie Heaps, Hash-Tabellen und dynamische Arrays (z. B. Java Vector).
- Algorithmen: Sie werden in einer Vielzahl von Algorithmen verwendet, darunter Sortier- und Suchalgorithmen, bei denen der zufällige Zugriff auf Elemente die Leistung erheblich optimiert.
Liste (Linked List)
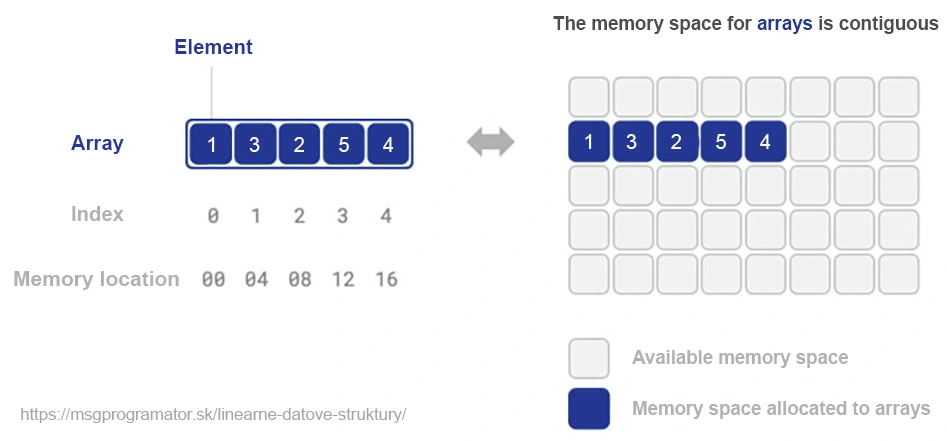
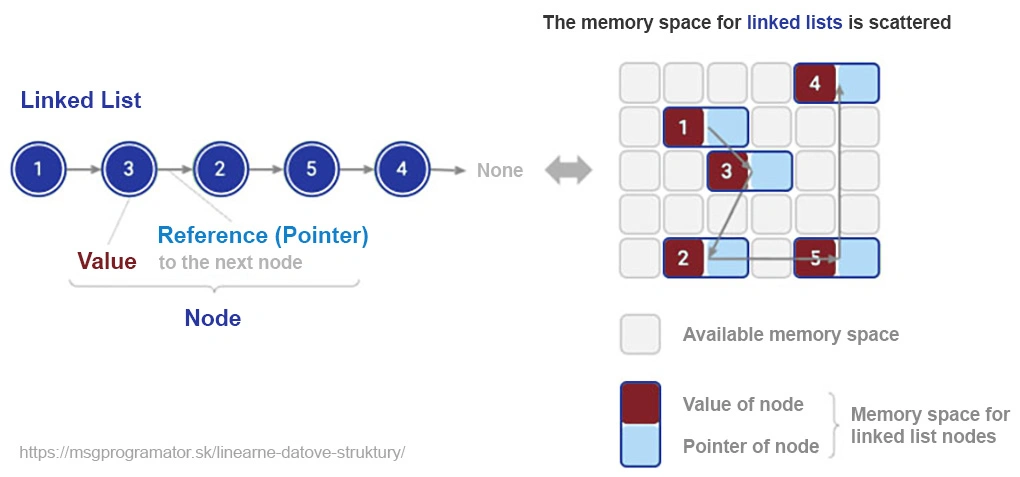
Eine verknüpfte Liste ist eine grundlegende Datenstruktur, die sich von einem Array durch ihre dynamische Natur und Flexibilität unterscheidet. Im Gegensatz zu Arrays, die einen zusammenhängenden Speicherblock benötigen, besteht eine verknüpfte Liste aus im Speicher verstreuten Knoten, wobei jeder Knoten einen Wert und einen Verweis (Pointer) auf den nächsten Knoten enthält. Diese Eigenschaft ermöglicht eine einfache Manipulation der Elemente, allerdings um den Preis einer geringeren Effizienz beim direkten Zugriff.
Grundlegende Listeneigenschaften
- Dynamische Größe: Die Größe der Liste ist nicht festgelegt und kann sich während der Programmlaufzeit dynamisch ändern – die Liste ist ideal für Anwendungen, bei denen die Größe der Daten nicht im Voraus bekannt ist.
- Verteilte Speicherzuweisung: Listenknoten werden nicht in zusammenhängenden Speicherblöcken gespeichert, sondern sind durch Links miteinander verbunden, so dass Elemente hinzugefügt und gelöscht werden können, ohne dass der Speicher neu angeordnet werden muss.
- Sequentieller Zugriff: Im Gegensatz zu Arrays, die einen direkten Zugriff auf Elemente über einen Index ermöglichen, muss eine Liste sequentiell vom Anfang bis zum gewünschten Knoten durchlaufen werden.
Arten von Listen
- Einzeln aufgeführte Liste: Jeder Knoten enthält einen Wert und einen Verweis auf den nächsten Knoten. Der letzte Knoten zeigt auf null, um das Ende der Liste anzuzeigen.
- Kreisförmig aufgelistete Liste (Circular listed list): der letzte Knoten zeigt zurück auf den ersten Knoten, wodurch ein Kreis entsteht – nützlich für Anwendungen, die einen wiederholten Zugriff auf Elemente erfordern.
- Doppelt gelistete Liste (Doubly listed list): Jeder Knoten enthält einen Verweis auf den vorherigen und den nächsten Knoten, so dass die Liste in beide Richtungen durchlaufen werden kann.
Vorteile der Verwendung einer Liste
- Effiziente Manipulation: Das Hinzufügen und Löschen von Elementen ist einfach und effizient, wenn wir den Verweis auf den Bearbeitungsort kennen, mit O(1) Zeitkomplexität.
- Flexibilität: Dank der dynamischen Größenanpassung muss die Kapazität nicht im Voraus festgelegt werden und Speicherplatzverschwendung wird vermieden.
- Implementierung komplexer Strukturen: Listen sind die Grundlage für andere Datenstrukturen wie Stapel, Warteschlangen und Graphen.
Nachteile der Verwendung einer Liste
- Langsamer Zugriff: Ein zufälliger Zugriff auf Elemente ist nicht möglich – jeder Zugriff erfordert eine Traversierung vom Anfang der Liste, was eine Zeitkomplexität von O(n) hat.
- Speicherverbrauch: Jeder Knoten benötigt zusätzlichen Speicher, um Referenzen zu speichern, was bei einer großen Anzahl kleiner Elemente ineffizient sein kann.
- Ein komplexerer Verwaltung: Die Zeigermanipulation beim Hinzufügen oder Löschen von Knoten kann fehleranfällig sein.
Verwendung der Liste
- Dynamische Datenstrukturen: Listen werden verwendet, wenn Daten häufig hinzugefügt oder entfernt werden, z.B. bei Aufgaben, bei denen sich die Anzahl der Elemente ständig ändert.
- Darstellung von mathematischen Strukturen: zur Darstellung von Polynomen oder anderen dynamischen Datensätzen.
- Implementierung von Stapeln und Warteschlangen: Viele Datenstrukturen sind auf verknüpften Listen aufgebaut.
- Garbage Collection: Algorithmen zur Speicherverwaltung, wie z.B. Mark-and-Sweep, verwenden Listen, um Speicherblöcke zu verwalten.
Beispiele für die Verwendung
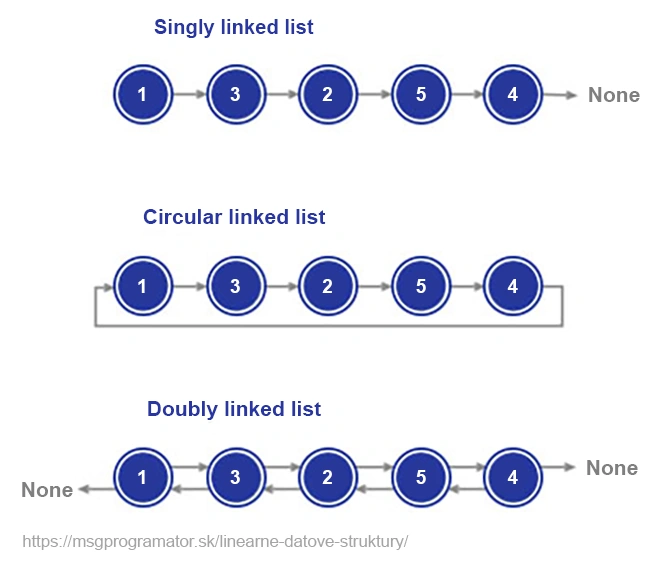
Stell dir die Historie eines Browsers vor. Jede besuchte Webseite wird als Knoten in einer Liste gespeichert. Wenn du zur vorherigen Seite zurückkehrst, bewegst du dich einfach zum vorherigen Knoten. Dies ist ein ideales Beispiel dafür, wie Listen ihre Stärke ausspielen. Listen sind unverzichtbar bei Aufgaben, die Flexibilität und dynamische Datenoperationen erfordern, obwohl sie nicht für alle Arten von Aufgaben geeignet sind.
Stapel (stack)
Der Stapel ist eine der grundlegenden Datenstrukturen, die nach dem Prinzip „Last In, First Out“ (LIFO) funktioniert. Stellen wir uns den Stapel wie einen Satz übereinander gestapelter Teller vor – wir fügen immer einen neuen Teller oben hinzu und greifen immer nach dem obersten, wenn wir ihn entfernen. Diese einfache, aber äußerst nützliche Struktur hat eine Vielzahl von Anwendungen in der Programmierung und der Computerwissenschaft.
Grundlegende Merkmale des Tabletts
- Top-only-Operationen: Alle Operationen (Hinzufügen und Entfernen eines Elements) werden am oberen Ende des Stapels durchgeführt, so dass der LIFO-Charakter erhalten bleibt.
- Dynamische Größe: Je nach Implementierung (z.B. bei Verwendung einer Liste) kann der Stack dynamisch wachsen oder schrumpfen, während das Programm läuft.
- Sequentieller Zugriff: Im Gegensatz zu Arrays hat der Stack keinen wahlfreien Zugriff – wir können nur direkt mit dem zuletzt eingefügten Element arbeiten.
Wichtige Stapeloperationen
- Push: Fügt ein Element an der Spitze des Stapels hinzu .
Pop:Entfernt ein Element von der Spitze des Stapels und gibt es wieder zurück.
Peek (Top): Zeigt das Element an der Spitze des Stapels an, ohne es zu entfernen.
IsEmpty: Prüft, ob der Stapel leer ist.
Vorteile der Verwendung eines Tabletts
- Geschwindigkeit der Operationen: Die Operationen des Hinzufügens und Entfernens von Elementen sind sehr effizient, mit einer Zeitkomplexität von O(1).
- Einfache Implementierung: Der Stack ist einfach zu verstehen und zu implementieren, egal ob Sie ein Array oder eine Liste verwenden.
- Spezifische Verwendung: Das Fach ist ideal für die Lösung von Problemen, bei denen eine LIFO-ähnliche Verarbeitungsreihenfolge eingehalten werden muss.
Nachteile der Verwendung eines Tabletts
- Eingeschränkter Zugriff: Der Zugriff ist nur auf das obere Element möglich, so dass es für Aufgaben, die einen direkten Zugriff erfordern, nicht geeignet ist.
- Speicherabhängigkeit: Im Falle einer Array-Implementierung kann der Stack eine Neuzuweisung von Speicher erfordern, wenn seine Kapazität seine ursprüngliche Größe übersteigt.
Verwendung des Tabletts
- Verwaltung von Funktionsaufrufen: Stacks werden zur Verwaltung von Funktionsaufrufen in Programmen verwendet. Jedes Mal, wenn eine Funktion aufgerufen wird, wird ihr Kontext auf dem Stack gespeichert und wiederhergestellt, wenn die Funktion beendet ist.
- Syntaxprüfung: Bei der Überprüfung der korrekten Einschließung von Klammern oder anderen gepaarten Symbolen im Code stellt der Stack sicher, dass die Reihenfolge korrekt ist.
- Backtracking-Algorithmen: werden für Aufgaben wie das Lösen von Labyrinthen oder Sudoku verwendet, bei denen man zu einem früheren Entscheidungspunkt zurückkehren muss.
- Implementierung von Rückgängig-Funktionen: In Anwendungen, in denen wir die letzte Aktion rückgängig machen wollen, speichert der Stack eine Historie der durchgeführten Aktionen.
Beispiel für die Verwendung
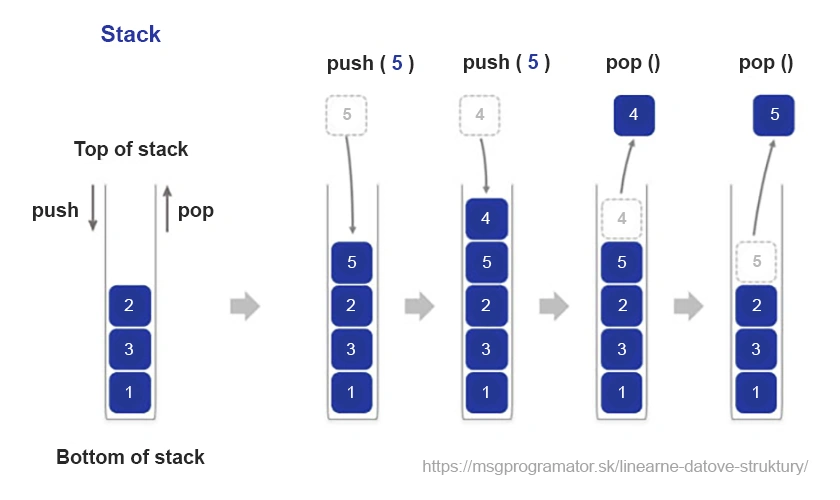
Stellen Sie sich einen Texteditor mit einer Zurück-Funktion vor. Jede Änderung, die wir vornehmen, wird dem Stapel hinzugefügt. Wenn wir auf „Rückgängig“ klicken, wird die letzte Änderung entfernt und unser Dokument kehrt in seinen vorherigen Zustand zurück.
Stacks sind zwar in ihrer Einfachheit und ihren Beschränkungen spezifisch, aber diese Eigenschaften machen sie in vielen Anwendungen und Algorithmen unverzichtbar, bei denen die Reihenfolge der Ausführung von Operationen genau eingehalten werden muss. Weitere Informationen findest du im Artikel über den Java Stack.
Front (Queue)
Eine Warteschlange ist eine grundlegende Datenstruktur, die nach dem FIFO-Prinzip (first in, first out) arbeitet. Man kann sie sich als eine Warteschlange von Aufträgen vorstellen, die darauf warten, verarbeitet zu werden – der erste, der eintrifft, wird auch als erster verarbeitet. Diese Struktur ist äußerst nützlich in Situationen, in denen es wichtig ist, die Reihenfolge der Verarbeitung einzuhalten.
Grundlegende Eigenschaften der Warteschlange
- Endoperationen: Neue Elemente werden am Ende hinzugefügt (enqueue) und vom Anfang entfernt (dequeue), so dass das FIFO-Verhalten erhalten bleibt.
- Dynamische Größe: Je nach Implementierung kann die Warteschlange wachsen oder schrumpfen, während das Programm läuft.
- Sequentieller Zugriff: Der Zugriff ist nur auf das Element am Anfang (vorne) oder am Ende (hinten) der Warteschlange möglich.
Die wichtigsten Funktionen der Front
- Enqueue: Fügt ein Element am Ende der Warteschlange hinzu.
Dequeue: Entfernt ein Element vom Anfang der Warteschlange und gibt es zurück.
Peek (Front): Zeigt das erste Element der Warteschlange an, ohne es zu entfernen.
IsEmpty: Prüft, ob die Warteschlange leer ist.
Front-Typen
- Einfache Warteschlange: klassische FIFO-Struktur, bei der Elemente am Ende hinzugefügt und am Anfang entfernt werden.
- Zirkuläre Warteschlange: eine effizientere Variante, die den freigewordenen Platz wiederverwendet, indem sie den letzten Index mit dem ersten zurückverknüpft.
- Prioritäts-Warteschlange: jedem Element wird eine Priorität zugewiesen und es wird entsprechend dieser Priorität verarbeitet, unabhängig von der Reihenfolge, in der es hinzugefügt wird.
- Doppelendige Warteschlange (Deque): ermöglicht das Hinzufügen und Entfernen von Elementen an beiden Enden.
Vorteile der Verwendung von Warteschlangen
- Order Preservation: ideal für Anwendungen, bei denen es wichtig ist, die Elemente in der Reihenfolge ihres Eingangs zu verarbeiten.
- Effizienz: Das Hinzufügen und Entfernen von Elementen ist zeitsparend, mit einer Zeitkomplexität von O(1), wenn es richtig implementiert ist (z.B. eine kreisförmige Warteschlange).
- Einfachheit: Das Warteschlangenkonzept ist einfach zu verstehen und zu implementieren.
Nachteile der Verwendung von Warteschlangen
- Eingeschränkter Zugriff: nur das erste und das letzte Element können manipuliert werden, so dass es für Aufgaben, die einen zufälligen Zugriff erfordern, ungeeignet ist.
- Ineffizienz des Speichers: Bei der Verwendung von Arrays kann eine einfache Warteschlange ineffizient sein, wenn der frei gewordene Speicherplatz nicht wiederverwendet wird.
Warteschlangen verwenden
- Prozessmanagement: Betriebssysteme verwenden Warteschlangen, um Prozesse zu planen, in denen Aufgaben in der Reihenfolge ihres Eintreffens auf ihre Ausführung warten.
- Verarbeitung von Datenströmen: In der Netzwerkkommunikation und beim Video-Streaming werden Warteschlangen verwendet, um den Empfang und die Verarbeitung von Daten zu steuern.
- Breadth-First Search: In Algorithmen wie der Breadth-First Search (BFS) bieten Warteschlangen eine sequentielle Suche nach benachbarten Knoten im Graphen.
- Anfragebearbeitung: Webserver oder Datenbanken verwenden Warteschlangen, um eingehende Anfragen (HTTP-Anfragen) in der Reihenfolge ihres Eingangs zu bearbeiten.
Beispiel für die Verwendung
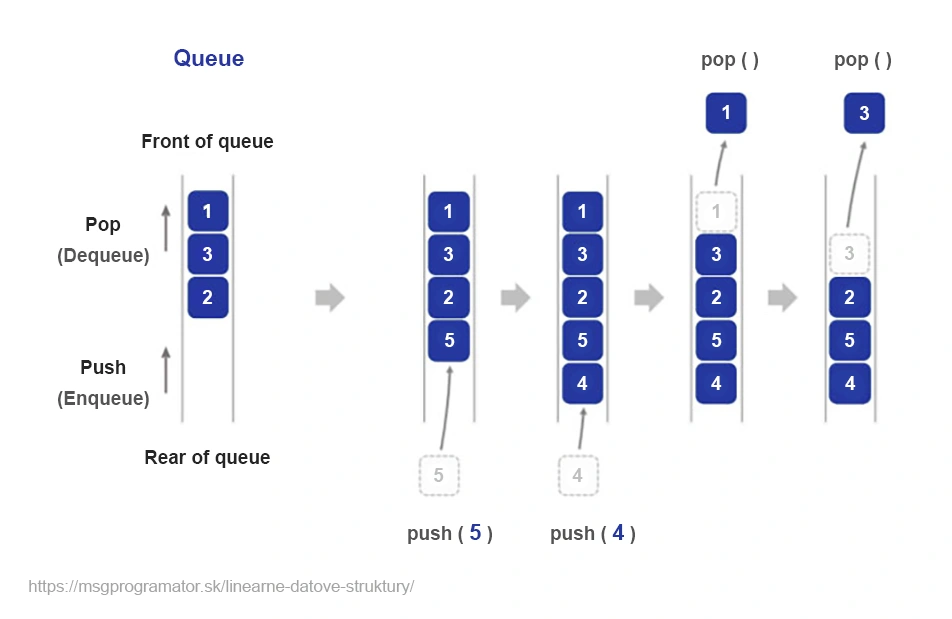
Stellen Sie sich eine Supermarktkasse vor. Jeder Kunde, der hereinkommt, steht am Ende der Warteschlange (enqueue). Der Kassierer bedient immer den Kunden, der am Anfang der Warteschlange steht (dequeue). Bei diesem Verfahren bleibt die Reihenfolge der Ankunft der Kunden erhalten.
Warteschlangen sind überall dort nützlich, wo Aufgaben oder Daten in der Reihenfolge ihres Eintreffens effizient verarbeitet werden müssen. Trotz der Einschränkungen, die ihr sequentieller Ansatz mit sich bringt, sind sie eine der wichtigsten Strukturen in der Programmierung.
Nichtlineare Datenstrukturen
Wir werden nun im Detail auf nicht-lineare Datenstrukturen, ihre grundlegenden Eigenschaften, Typen, Vor- und Nachteile sowie die häufigsten Anwendungsfälle/Beispiele eingehen.
Baum
Ein Baum ist eine grundlegende nichtlineare Datenstruktur, die Daten hierarchisch organisiert. Sie besteht aus Knoten, wobei jeder Knoten einen übergeordneten Knoten – den Parent – hat (mit Ausnahme des Root-Knotens) und null oder mehr Child-Knoten – die Children – haben kann. Diese Struktur ermöglicht eine effiziente Datenverarbeitung, insbesondere beim Suchen, Sortieren und Darstellen von Beziehungen.
Grundlegende Merkmale des Baums
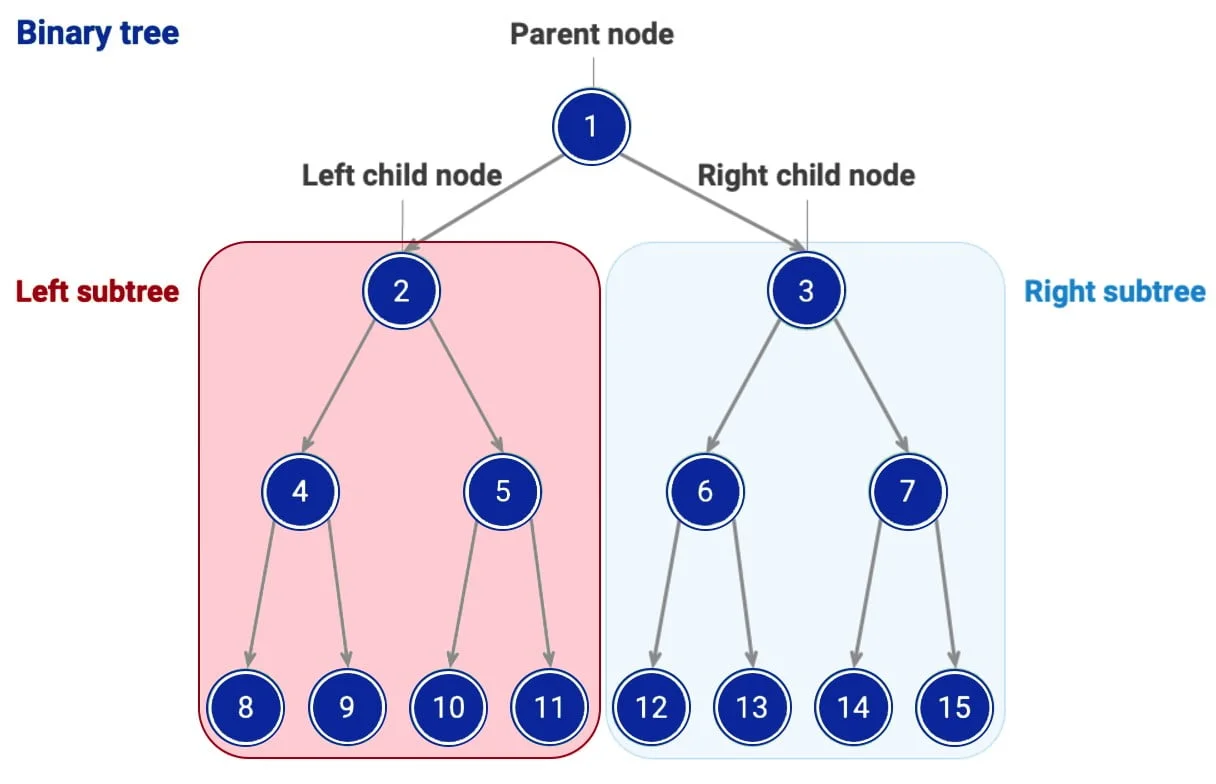
Hierarchische Struktur: Bäume sind in hierarchischen Ebenen angeordnet, wobei die Wurzel an der Spitze steht und die Knoten darunter die nächsten Ebenen darstellen.
Knoten und Kanten: Jeder Knoten enthält Daten und Links zu seinen Unterknoten. Kanten stellen Verbindungen zwischen Knoten dar.
Wurzel: Dies ist der höchste Knoten eines Baums, der keinen übergeordneten Knoten hat.
Blätter: sind Knoten, die keine Kinder haben (auch als Endknoten bekannt).
Höhe des Baums: Die Anzahl der Kanten auf dem längsten Pfad von der Wurzel zum Blatt.
Arten von Bäumen
Binärer Baum: jeder Knoten kann höchstens zwei Nachkommen haben – einen linken und einen rechten Knoten.
Binärer Suchbaum (BST): ein binärer Baum, bei dem die linken Teilbäume Werte enthalten, die kleiner als ein Knoten sind, und die rechten Teilbäume Werte enthalten, die größer als ein Knoten sind.
Ausgewogene Bäume: Bäume, wie z.B. AVL oder rot-schwarze Bäume, die eine ausgewogene Höhe für einen effizienteren Betrieb haben.
N-ärer Baum: Knoten können bis zu N Kindknoten haben.
Trie: Spezialisierter Baum für die effiziente Suche, zum Beispiel bei der Arbeit mit Wörtern oder Präfixen.
Vorteile der Verwendung eines Baumes
- Effizientes Suchen und Sortieren: Bäume, insbesondere binäre Suchbäume, ermöglichen ein schnelles Suchen und Organisieren von Daten.
- Flexibilität der Darstellung: Sie ermöglichen die Modellierung hierarchischer Beziehungen, wie z.B. Organisationsstrukturen, Dateisysteme oder Taxonomien.
- Dynamische Natur: Bäume können wachsen oder schrumpfen und haben keine feste Größe.
Nachteile der Verwendung eines Baumes
- Komplexere Implementierung: Die Arbeit mit Bäumen erfordert die Verwaltung von Zeigern auf Baumknoten, was fehleranfällig sein kann.
- Speicherbedarf: Jeder Knoten benötigt zusätzlichen Speicher für Verweise auf seine Unterknoten.
- Ineffizienz bei unausgewogenen Bäumen: Bäume, die unausgewogen sind, können zu einer linearen Struktur degradieren, was zu einer verminderten Leistung bei O(n) führt.
Verwendung von Bäumen
- Datenbankindizes: B-Bäume und ihre Varianten werden für die effiziente Suche und Verwaltung großer Datenmengen verwendet.
- Dateisysteme: Bäume stellen die Struktur von Ordnern und Dateien auf einer Festplatte dar.
- Pfadfindung in Graphen: Bäume sind die Grundlage von Algorithmen zur Pfadfindung oder Graphenabdeckung.
- Datenkompression: Huffman-Bäume werden in Kompressionsalgorithmen wie zip oder gzip verwendet.
Beispiel für die Verwendung
Stellen Sie sich einen Stammbaum vor – die Wurzel des Baumes steht für den ältesten Vorfahren und die Knoten darunter für dessen Nachkommen. Diese Hierarchie ist ein direktes Beispiel für die Verwendung eines Baums zur Organisation und klaren Darstellung von Daten.
Bäume sind eine der wichtigsten Datenstrukturen in der Computerwissenschaft. Ihre Fähigkeit, komplexe Beziehungen zu modellieren und hierarchische Daten effizient zu bearbeiten, macht sie zu einem integralen Bestandteil moderner Algorithmen und Anwendungen.
Graph (Graph)
Ein Graph ist eine nichtlineare Datenstruktur, die Objekte (Knoten, auch als Eckpunkte bezeichnet) und die Beziehungen zwischen ihnen (genannt Kanten) darstellt. Diese Struktur ist äußerst vielseitig und wird verwendet, um verschiedene Situationen zu modellieren, wie soziale Netzwerke, Verkehrskarten oder Beziehungen zwischen Entitäten in Datenbanken.
Grundlegende Chart-Eigenschaften
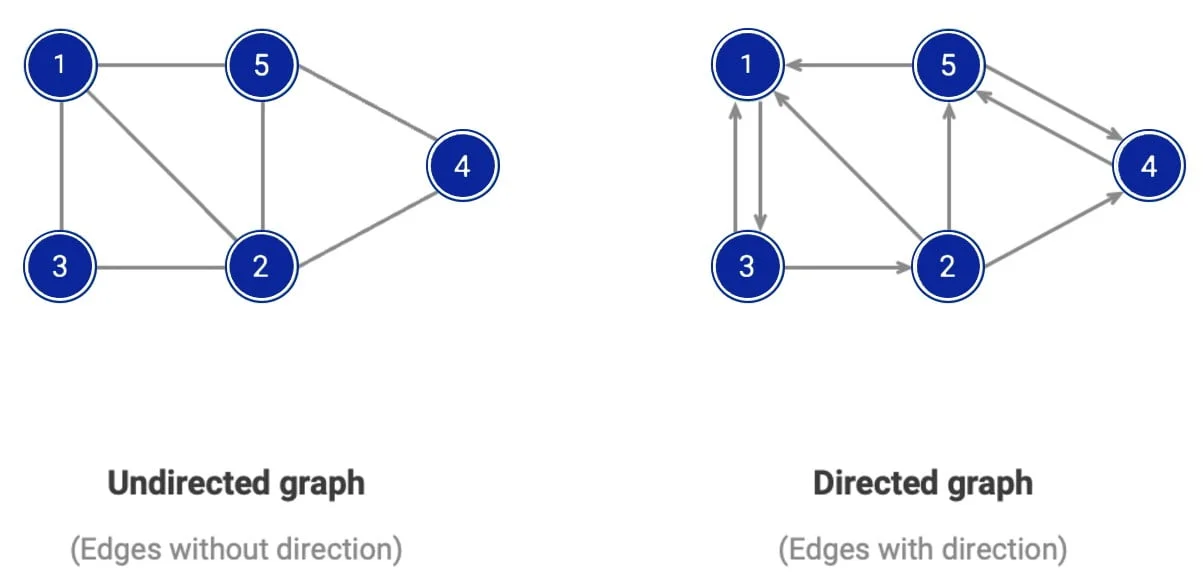
Vertices (Knoten): die grundlegenden Teile des Graphen, die Objekte oder Entitäten darstellen.
Kanten: Verbindungen zwischen Eckpunkten, die Beziehungen oder Interaktionen darstellen.
Orientierung: Der Graph kann orientiert sein (gerichtete Kanten, z. B. eine Einbahnstraße) oder nicht orientiert (keine Richtung, z. B. eine Straße mit zwei Richtungen).
Kantengewichtung: Einige Diagramme enthalten Gewichtungen an den Kanten, um Werte wie Entfernungen, Kosten oder Zeit darzustellen.
Arten von Diagrammen
Ungerichtetes Diagramm: Kanten haben keine Richtung, die Verbindung zwischen zwei Eckpunkten ist gegenseitig.
Gerichtetes Diagramm oder Digraph: Kanten haben eine Richtung und verbinden Eckpunkte in einer bestimmten Reihenfolge.
Gewichteter Graph: den Kanten wird ein Wert (Gewicht) zugewiesen.
Zyklischer Graph: enthält geschlossene Pfade (Zyklen).
Azyklischer Graph: enthält keine Zyklen.
Baumdiagramm oder Baum: ein Spezialfall eines azyklischen Graphen, bei dem jeder Knoten über einen einzigen Pfad zugänglich ist.
Verbundener Graph: es gibt einen Pfad zwischen zwei Knotenpunkten.
Vorteile der Verwendung von Diagrammen
- Flexibilität der Darstellung: Graphen eignen sich für die Modellierung jeder Beziehung, von Netzwerktopologien bis hin zu menschlichen Interaktionen.
- Effiziente Suche: Viele Algorithmen sind für die Arbeit mit Graphen optimiert, wie z.B. Dijkstras Algorithmus zum Auffinden des kürzesten Pfades.
- Visualisierungsoption: Diagramme sind intuitiv zu verstehen und visuell zu interpretieren, was die Datenanalyse erleichtert.
Nachteile der Verwendung von Diagrammen
- Speicherverbrauch: Das Speichern großer Graphen, insbesondere wenn sie dicht sind, kann sehr speicherintensiv sein.
- Komplexität der Vorgänge: Die Implementierung und Verwaltung von Diagrammen kann komplex sein, insbesondere bei dynamischen Änderungen.
- Potenzielle Ineffizienz: Einige Graphenalgorithmen haben eine hohe Zeitkomplexität, was bei großen Graphen problematisch sein kann.
Verwendung von Diagrammen
- Soziale Netzwerke: Modellierung von Beziehungen zwischen Benutzern, wie Freundschaften oder Follower.
- Schifffahrt und Verkehr: Darstellung von Straßen, Eisenbahnstrecken oder Flugrouten.
- Prozessoptimierung: Finden des effizientesten Pfades, des Baumes mit den geringsten Kosten oder des maximalen Flusses.
- Webcrawler: Suchmaschinen verwenden Diagramme, um die Verbindungen zwischen Webseiten zu indizieren und zu analysieren.
- Biologie und chemische Strukturen: Darstellung von Molekülen, Gennetzwerken oder evolutionären Beziehungen.
Beispiel für die Verwendung
Stellen Sie sich ein städtisches Verkehrsnetz vor. Jeder Ort (Haltestelle) ist ein Knoten und die Verbindung zwischen Haltestellen ist eine Kante. Um den schnellsten Weg zwischen zwei Orten zu finden, verwenden wir einen Algorithmus, der den Graphen durchläuft und die kürzeste Route ermittelt.
Graphen sind unverzichtbar bei der Lösung komplexer Probleme, bei denen es darauf ankommt, die Beziehungen zwischen Objekten zu verstehen und analysieren zu können. Dank ihrer Vielseitigkeit und der reichhaltigen Möglichkeiten ihrer Anwendung sind sie zur Grundlage vieler Bereiche der modernen Computerwissenschaft geworden.
Tabellarische Datenstrukturen
Jetzt werden wir die tabellarischen Datenstrukturen, ihre grundlegenden Eigenschaften, Typen, Vor- und Nachteile sowie die häufigsten Anwendungsfälle/Beispiele im Detail besprechen.
Hash-Tabelle
Eine Hashtabelle ist eine Datenstruktur, die ein assoziatives Array implementiert, in dem Werte (Daten) anhand eines eindeutigen Schlüssels gespeichert und abgerufen werden. Sie verwendet eine Hash-Funktion, die den Schlüssel in einen Index im Array umwandelt und so eine effiziente Speicherung und den Zugriff auf die Daten ermöglicht.
Grundlegende Merkmale der Hashtabelle
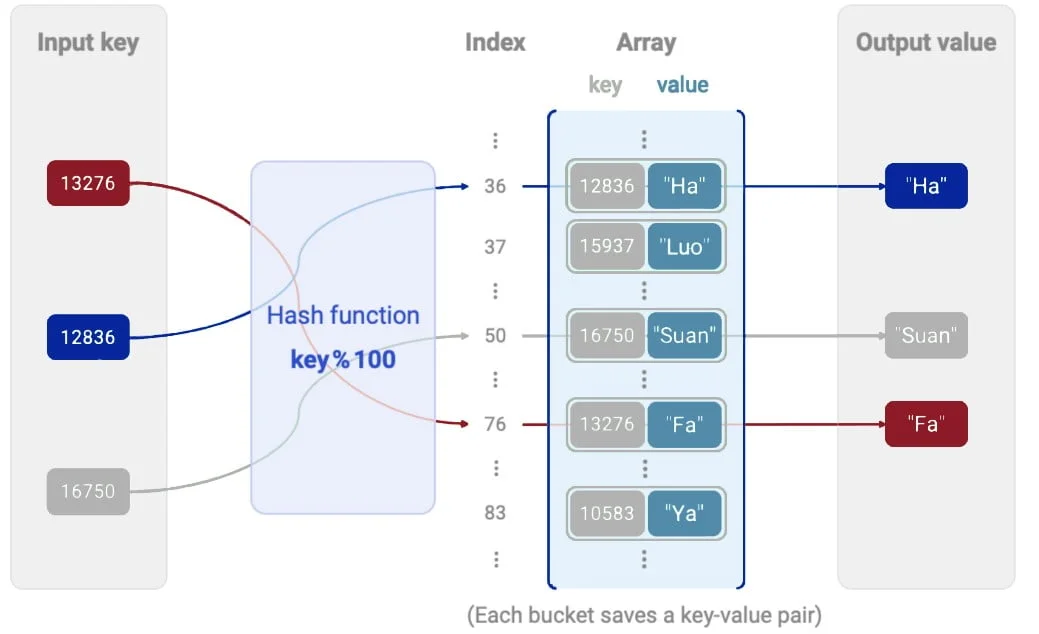
Hash-Funktion: Der Schlüssel wird mithilfe dieser Funktion in einen Index im entsprechenden Feld umgewandelt. Die Qualität der Hash-Funktion bestimmt die Leistung der Tabelle.
Eindeutige Schlüssel: jedem Datensatz in der Tabelle wird ein eindeutiger Schlüssel zugewiesen.
Kollisionen: Wenn zwei verschiedene Schlüssel denselben Index erzeugen, kommt es zu einer Kollision, die durch spezielle Techniken (z.B. getrennte Verkettung) aufgelöst wird.
Auflösung von Kollisionen
Getrennte Verkettung: Jeder Index in der Tabelle enthält eine Liste oder eine andere Struktur, die alle Werte mit demselben Index speichert.
Offene Adressierung: Wenn eine Kollision auftritt, wird ein anderer freier Steckplatz nach einem bestimmten Muster gesucht (z.B. lineares oder quadratisches Probing).
Vorteile der Verwendung einer Hashtabelle
- Geschwindigkeit der Operationen: Idealerweise haben Such-, Einfüge- und Löschoperationen eine Zeitkomplexität von O(1).
- Effiziente Nutzung des Speichers: Die Tabelle verwaltet den Speicherplatz dynamisch entsprechend der Anzahl der gespeicherten Elemente.
- Einfacher Zugriff auf Daten: Ermöglicht einen effizienten Abgleich und eine schnelle, schlüsselbasierte Suche.
Nachteile der Verwendung einer Hashtabelle
- Abhängigkeit von der Hash-Funktion: Eine schwache Funktion kann zu häufigen Kollisionen und verminderter Leistung führen.
- Speicherbedarf: Bei einer großen Anzahl von Schlüsseln kann eine große Menge an Speicher benötigt werden.
- Unorganisierte Daten: Die Tabelle behält die Reihenfolge der Datensätze nicht bei, was in einigen Anwendungen nachteilig sein kann.
Verwendung der Hashtabelle
- Schnellsuche: wird in den meisten Programmiersprachen zur Implementierung von Maps, Dictionaries und assoziativen Arrays verwendet.
- Caching: Tabellen sind die Grundlage von Caches, bei denen der schnelle Zugriff auf häufig verwendete Daten entscheidend ist.
- Erkennung von Duplikaten: erkennt schnell, ob ein Element bereits existiert, was für Filter wie den Bloom-Filter nützlich ist.
- Datenbankindizes: werden verwendet, um den Zugriff auf Daten in Datenbanken zu optimieren.
- Verschlüsselung: Hash-Funktionen sind der Schlüssel zur Erzeugung eindeutiger Prüfsummen.
Beispiel für die Verwendung
Stellen Sie sich ein Telefonbuch vor, in dem Sie schnell die Nummer einer Person anhand ihres Namens nachschlagen möchten. Der Name der Person dient als Schlüssel, der mithilfe der Hash-Funktion in einen Index umgewandelt wird. Die entsprechende Telefonnummer wird in diesem Index gespeichert.
Hash-Tabellen sind eine leistungsstarke und effiziente Struktur für eine Vielzahl von Anwendungen, bei denen der schnelle Zugriff auf Daten eine Priorität ist. Ihre Fähigkeit, große Datenmengen effizient zu verarbeiten, macht sie im gesamten IT-Bereich unverzichtbar.
Andere Datenstrukturen
Ich möchte noch kurz einige der weniger bekannten Datenstrukturen erwähnen, die uns in der IT begegnen können.
Heap
Ein binärer Baum, der die folgende Bedingung erfüllt (jeder übergeordnete Knoten ist größer oder kleiner als seine Kinder). Er wird zur Implementierung von Prioritätswarteschlangen oder in einem Algorithmus verwendet Heap Sortverwendet, den wir bereits in unserem Blog vorgestellt haben.
Trie (Präfixbaum)
Ein Trie ist eine für die Stringsuche optimierte Baumtabellenstruktur, bei der jeder Knoten einen Teil eines Schlüssels darstellt. Sie wird in Textverarbeitungsprogrammen, bei der automatischen Vervollständigung oder bei der Suche in Datenbanken verwendet.
Disjunkte Menge
Es wird verwendet, um Mengen mit disjunkten Elementen darzustellen und zu verwalten. Er wird in Graph-Algorithmen wie dem Kruskal-Algorithmus verwendet.
Segmentbaum (Intervallbaum)
Ein Baum, der entwickelt wurde, um Probleme im Zusammenhang mit Intervallen und Datenbereichen effizient zu lösen. Er eignet sich für schnelle Operationen zur Bestimmung der Summe, des Minimums oder des Maximums eines Bereichs.
Fenwick Baum
Effiziente Struktur zum Aktualisieren und Suchen von Summen in Sequenzen. Sie wird in Aufgaben verwendet, die Bereiche berechnen.
K-D Tree (K-Dimensionaler Baum)
Ein spezialisierter Baum zum Organisieren von Punkten im K-dimensionalen Raum. Er wird in Algorithmen für Bildverarbeitung, Computer Vision und Datenbanksuche verwendet.
Suffix Baum
Stellt alle Suffixe einer gegebenen Zeichenkette dar. Es ist besonders effektiv bei der Teilstringsuche und textbasierten Algorithmen.
Matrix-Tabelle
Matrixtabellen sind zwei- oder mehrdimensionale Arrays, die Daten in Zeilen und Spalten speichern. Sie werden z.B. in der linearen Algebra für die Arbeit mit Matrizen verwendet.
Adjacency Matrix
Eine zweidimensionale Matrix, bei der die Zeilen und Spalten die Eckpunkte des Graphen darstellen und die Werte in der Matrix die Existenz von Kanten zwischen den Eckpunkten anzeigen. Sie wird verwendet, um dichte Graphen effizient darzustellen und das Vorhandensein einer Kante zwischen zwei Scheitelpunkten schnell zu erkennen.
Adjacency List (Nachbarschaftsliste):
Eine Liste, in der jeder Scheitelpunkt des Graphen eine Liste aller benachbarten Scheitelpunkte enthält. Ideal für die Darstellung spärlicher Graphen, da sie im Vergleich zu einer Nachbarschaftsmatrix Speicherplatz spart.
Sparse Matrix (Spärliche Matrix)
Struktur zum Speichern von Matrizen mit den meisten Nullwerten, wobei nur Nicht-Nullwerte und ihre Positionen gespeichert werden. Sie wird in Bereichen wie dem maschinellen Lernen, der Graphenanalyse und der Modellierung großer spärlicher Datenstrukturen verwendet.
Scatter Table (Streutabellen):
Eine hashtabellenähnliche Struktur, die Kollisionen auf eine alternative Weise der Schlüsselverteilung auflöst. Effizient bei der Verarbeitung großer Datenmengen mit geringerem Risiko von Clusterkollisionen in Hash-Strukturen.
Fazit
Datenstrukturen sind ein wesentlicher Bestandteil der Programmierung, da sie eine Möglichkeit bieten, Daten effizient zu organisieren, zu verarbeiten und zu manipulieren. Lineare Datenstrukturen (Warteschlange, Stack, verknüpfte Liste, Array) haben spezifische Vor- und Nachteile und Anwendungsbereiche.
Ihre richtige Auswahl und Implementierung kann die Leistung und Effizienz der Software erheblich beeinflussen. Daher ist das Verständnis der grundlegenden Prinzipien von Datenstrukturen für jeden, der sich tiefer mit Programmierung, Algorithmen oder Datenbanken befassen möchte, von entscheidender Bedeutung, damit er dieses Wissen nutzen kann, um optimierte und innovative Lösungen zu entwickeln.
Wenn Sie auf der Suche nach einem Job sind und ein Java-Programmierer sind, informieren Sie sich über unsere Mitarbeitervorteile und reagieren Sie auf unsere aktuellen Stellenausschreibungen.
