Java Entwickler Experte
Merge sort – Sortieren durch Aufteilen und Zusammenführen in Java
Sortieralgorithmen werden verwendet, um die Elemente eines Arrays oder einer Liste in aufsteigender oder absteigender numerischer oder lexikografischer Reihenfolge neu zu ordnen. Die Sortierung ist sehr wichtig für die optimale Leistung anderer Algorithmen, die sortierte Eingabedaten benötigen. Es gibt eine Reihe von verschiedenen Sortieralgorithmen. Die Auswahl eines geeigneten Algorithmus hängt von Faktoren wie der Größe und den Eigenschaften der Eingabedaten, dem verfügbaren Speicher und den Zeit- und Platzanforderungen ab. Um dir die Auswahl zu erleichtern, werden wir in unserer Serie die bekanntesten Datensortieralgorithmen nacheinander vorstellen, ihre Prinzipien, Vor- und Nachteile erklären und sie in Java programmieren. Bislang haben wir die folgenden Sortieralgorithmen behandelt:
In diesem Artikel erfährst du:
- Sortieralgorithmen: eine Einführung in das Sortieren von Daten,
- Bubble sort – Blasen-Sortierung,
- Comb sort – Kamm-Sortierung,
- Big O Notation: Analyse der Komplexität von Algorithmen,
- Selection sort – triedenie výberom.
- Insertion sort – Sortieren durch Einfügen
- Counting sort – Sortieren durch Zählen
- Heap sort – Heap-Sortierung
Heute werden wir uns mit dem Sortieren durch Zusammenführen – Merge Sort – befassen.
Merge sort
Merge Sort ist ein sehr effizienter stabiler Sortieralgorithmus, der 1945 von John von Neumann, einem der Pioniere auf dem Gebiet der Informatik, erfunden wurde. Der Grundgedanke dabei ist, dass wir bei einem komplexen Problem versuchen, es in kleinere Teile zu zerlegen und diese Teile separat zu lösen. Die endgültige Lösung ist also das Ergebnis der Lösung jedes der kleineren Teilprobleme. Eine solche Zerlegung von Problemen kann dann perfekt parallelisiert und auf modernen Mehrkernprozessoren effizient gelöst werden. Wir unterteilen den Eingabedatenvektor in mehrere annähernd gleiche Teile. Die gebräuchlichste Version verwendet eine 2-teilige Partitionierung, das ist eine binäre Zusammenführung, im Falle von mehreren Teilen ist es eine sogenannte K-way Zusammenführung. Sehen wir uns an, wie diese Technik bei der Datensortierung eingesetzt werden kann.
Merge sort Algorithmus – Funktionsprinzip
Die Eingabedaten werden in etwa zwei gleiche Teile geteilt. Wenn die Anzahl der Elemente ungerade ist, enthält der erste Teil 1 Element mehr. Jeder dieser Teile des Arrays wird weiter in zwei Hälften geteilt und dies wird wiederholt, bis der Teil nur noch ein Element enthält. Dabei wird ein rekursiver Aufruf verwendet. Ein Array mit einem Element wird als sortiert betrachtet. Sobald die Teile nicht mehr geteilt werden können, werden die letzten beiden Hälften genommen und ihre Elemente zusammengeführt, so dass die resultierende Liste ebenfalls sortiert bleibt. Dies wird so lange wiederholt, bis der ursprüngliche Datenvektor in sortierter Form erhalten wird. Dies lässt sich am besten anhand des Beispiels in der folgenden Abbildung nachvollziehen.
Merge sort Animation, Visualisierung, gif
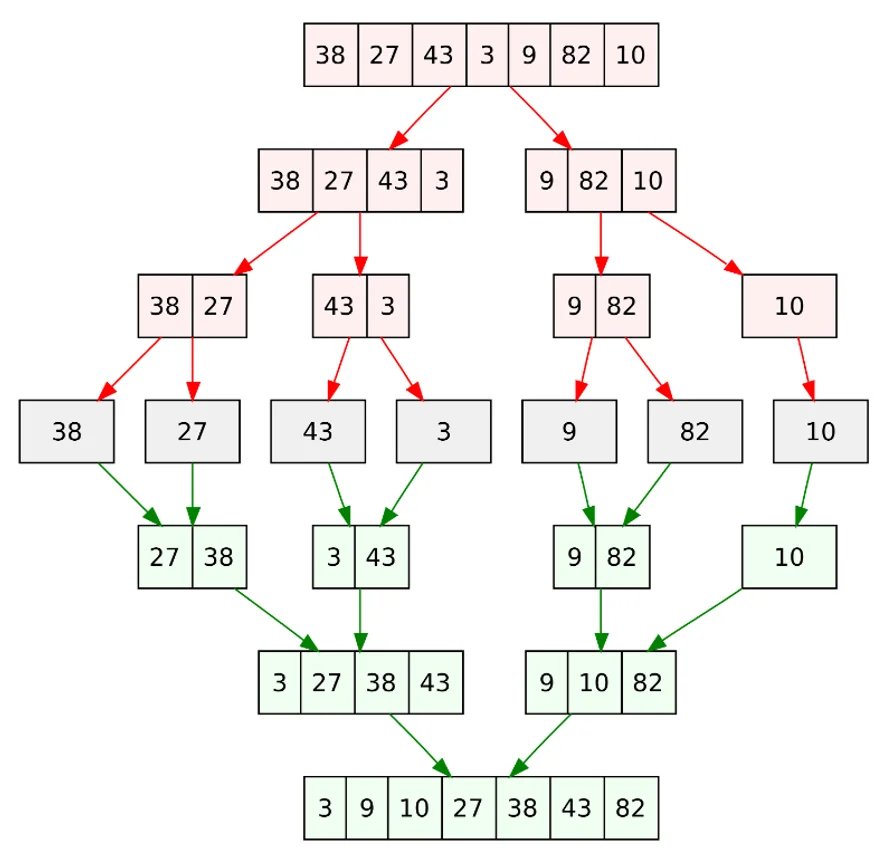
Die Animation für merge sort sieht so aus:
Quelle: commons.wikimedia.org/wiki/Category:Animations_of_sort_algorithms
Eine Animation des Algorithmus findest du z.B. auf Toptal. Es gibt 8 Arten von Algorithmen, du kannst die Animation auch rückwärts abspielen. Auf dieser Seite kannst du die Schritte des Algorithmus durchlaufen, so dass du den Zeitverbrauch des Algorithmus überprüfen kannst.
Vorteile des Merge sort Algorithmus
- Stabiler Algorithmus
- Effizient auch bei großen Datensätzen
- Kann leicht parallelisiert werden, um die Berechnungslast auf mehrere Prozessoren zu verteilen
Nachteile des Merge sort Algorithmus
- Beim Zusammenführen von Subarrays wird zusätzlicher Speicherplatz zum Speichern von Daten benötigt
Merge Sort – Zeitkomplexität
| Algorithmus | Methode | Zeitliche Komplexität | Speicher | Stabil | ||
| schlechteste | durchschnittlich | beste | ||||
| Merge sort | merge | O(n log n) | O(n log n) | O(n log n) | O(n) | Ja |
Merge Sort Implementierung, Java Code
Jetzt werden wir die Implementierung des Merge sort algorithmus in Java zeigen.
MergeSort.java
package sorting;
public class MergeSort {
public void sort(int data[], int left, int right)
{
if (left < right) {
// Find the cutting point
int middle = (left + right) / 2;
// Sort first and second part separately
sort(data, left, middle);
sort(data, middle + 1, right);
// Merge both sorted halves
merge(data, left, middle, right);
}
}
public void merge(int[] data, int left, int middle, int right) {
// Calculate sizes of left and right merge arrays
int leftPartSize = middle - left + 1;
int rightPartSize = right - middle;
// Create them
int[] leftPart = new int[leftPartSize];
int[] rightPart = new int[rightPartSize];
// Fill them
for (int i = 0; i < leftPartSize; i++) {
leftPart[i] = data[left + i];
}
for (int j = 0; j < rightPartSize; j++) {
rightPart[j] = data[middle + 1 + j];
}
System.out.print("L: ");
printArray(leftPart);
System.out.print("+ R: ");
printArray(rightPart);
System.out.print("=> ");
// k is index of merged array
int i = 0, j = 0, k = left;
while (i < leftPartSize && j < rightPartSize) {
if (leftPart[i] <= rightPart[j]) {
data[k++] = leftPart[i++];
}
else {
data[k++] = rightPart[j++];
}
}
// Copy any remaining elements
while (i < leftPartSize) {
data[k++] = leftPart[i++];
}
while (j < rightPartSize) {
data[k++] = rightPart[j++];
}
for (i = left; i < k; i++)
System.out.print(data[i] + " ");
System.out.println();
}
// Function to print an array
public void printArray(int data[])
{
for (int i = 0; i < data.length; i++)
System.out.print(data[i] + " ");
//System.out.println();
}
}Main.java
import sorting.MergeSort;
public class Main {
public static void main(String[] args) {
int dataToSort[] = { 6, 5, 4, 2, 3, 1, 7 };
MergeSort mergeSort = new MergeSort();
System.out.print("Input: ");
mergeSort.printArray(dataToSort);
System.out.println("");
mergeSort.sort(dataToSort, 0, dataToSort.length - 1);
System.out.print("Sorted: ");
mergeSort.printArray(dataToSort);
}
}Die Ausgabe dieses Beispiels ist:
Wir haben die Dateien mit dem obigen Beispiel in Form von Code vorbereitet, den du direkt in Java ausführen kannst. Lade den Merge Sort Java-Code hier herunter.
Wenn du ein Java Programmierer bist und nach Arbeit suchst, schau dir unsere Mitareiterbenefits an und reagiere auf die neuesten Stellenangebote.
